
【题目】已知:A=![]() ,B=
,B=![]()
(1)求3A+6B;
(2)若3A+6B的值与a的取值无关,求b的值.
科目:初中数学 来源: 题型:
【题目】已知抛物线y=kx2+(k﹣2)x﹣2(其中k>0).
(1)求该抛物线与x轴的交点及顶点的坐标(可以用含k的代数式表示);
(2)若记该抛物线顶点的坐标为P(m,n),直接写出|n|的最小值;
(3)将该抛物线先向右平移![]() 个单位长度,再向上平移
个单位长度,再向上平移![]() 个单位长度,随着k的变化,平移后的抛物线的顶点都在某个新函数的图象上,求新函数的解析式(不要求写自变量的取值范围).
个单位长度,随着k的变化,平移后的抛物线的顶点都在某个新函数的图象上,求新函数的解析式(不要求写自变量的取值范围).
查看答案和解析>>
科目:初中数学 来源: 题型:
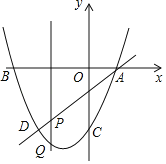
【题目】如图,抛物线y=ax2+bx﹣3过A(1,0),B(﹣3,0),直线AD交抛物线于点D,点D的横坐标为﹣2,点P(m,n)是线段AD上的动点.
(1)求直线AD及抛物线的解析式;
(2)过点P的直线垂直于x轴,交抛物线于点Q,求线段PQ的长度l与m的关系式,m为何值时,PQ最长?
(3)在平面内是否存在整点(横、纵坐标都为整数)R,使得P,Q,D,R为顶点的四边形是平行四边形?若存在,直接写出点R的坐标;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD、CF分别是∠BAC、∠ACB的角平分线,且AD、CF交于点I,IE⊥BC与E,下列结论:①∠BIE=∠CID;②S△ABC=![]() IE(AB+BC+AC);③BE=
IE(AB+BC+AC);③BE=![]() (AB+BC-AC);④AC=AF+DC.其中正确的结论是( )
(AB+BC-AC);④AC=AF+DC.其中正确的结论是( )

A. ①②③ B. ①②④ C. ②③④ D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
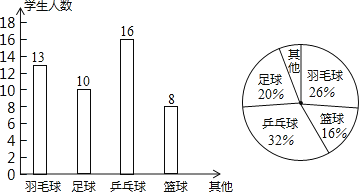
【题目】某校为了组织一次球类对抗赛,在本校随机抽取了若干名学生,对他们每个人最喜欢的一项球类运动进行了统计,将调查结果整理后绘制成如图所示的不完整的统计图,请你依据以上的信息回答下列问题:
(1)求本次被调查的学生人数;
(2)通过计算补全条形统计图;
(3)若全校有4000名学生,请你估计该校最喜欢篮球和足球运动的学生共有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
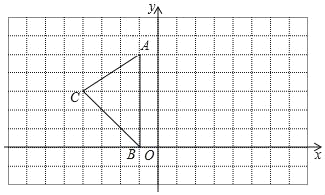
【题目】如图,在平面直角坐标系中,A(﹣1,5),B(﹣1,0),C(﹣4,3)
(1)在图中作出△ABC关于y轴的对称图形△A1B1C1;
(2)求出△A1B1C1的面积;
(3)将△ABC向左平移2个单位,再向上平移2个单位得△A2B2C2,请直接写出点A2,B2,C2的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在正方形ABCD中,P是对角线AC上的一点,点E在BC的延长线上,且PE=PB.
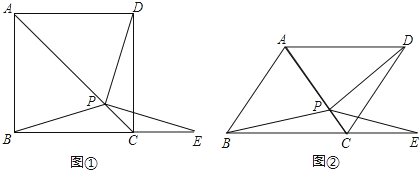
(1)求证:△BCP≌△DCP;
(2)求证:∠DPE=∠ABC;
(3)把正方形ABCD改为菱形,其它条件不变(如图②),若∠ABC=58°,则∠DPE= 度.
查看答案和解析>>
科目:初中数学 来源: 题型:
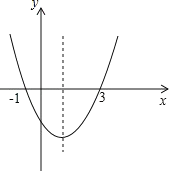
【题目】如图,二次函数 y=ax2+bx+c 的图象与 x 轴的交点的横坐标分别为-1,3,则:
①ac<0;②2a+b=0;③4a+2b+c>0;④对于任意 x 均有 ax2+bx≥a+b,其中结论正确的个数有( )
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
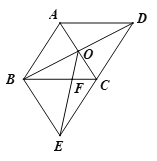
【题目】如图,菱形ABCD的对角线AC,BD相交于点O,∠ABC=60°,过点B作AC的平行线交DC的延长线于点E.
(1) 求证:四边形ABEC为菱形;
(2) 若AB=6,连接OE,求OE的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com