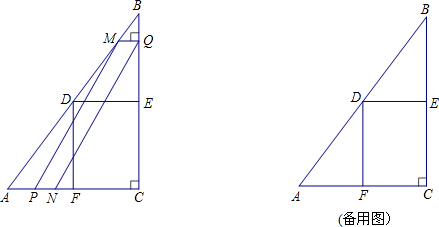
试题分析:(1)因为点A
0(0,0)在抛物线y
1=-(x-a
1)
2+a
1上,可求得a
1=1,则y
1=-(x-1)
2+1;令y
1=0,求得A
1(2,0),b
1=2;再由点A
1(2,0)在抛物线y
2=-(x-a
2)
2+a
2上,求得a
2=4,y
2=-(x-4)
2+4.
(2)求得y
1的顶点坐标(1,1),y
2的顶点坐标(4,4),y
3的顶点坐标(9,9),依此类推,y
n的顶点坐标为(n
2,n
2).因为所有抛物线顶点的横坐标等于纵坐标,所以顶点坐标满足的函数关系式是:y=x.
(3)①由A
0(0,0),A
1(2,0),求得A
0A
1=2;y
n=-(x-n
2)
2+n
2,令y
n=0,求得A
n-1(n
2-n,0),A
n(n
2+n,0),所以A
n-1A
n=(n
2+n)-(n
2-n)=2n;
②设直线解析式为:y=kx-2k,设直线y=kx-2k与抛物线y
n=-(x-n
2)
2+n
2交于E(x
1,y
1),F(x
2,y
2)两点,联立两式得一元二次方程,得到x
1+x
2=2n
2-k,x
1•x
2=n
4-n
2-2k.然后作辅助线,构造直角三角形,求出EF
2的表述式为:EF
2=(k
2+1)[4n
2•(1-k)+k
2+8k],可见当k=1时,EF
2=18为定值.所以满足条件的直线为:y=x-2.
试题解析:(1)∵当n=1时,第1条抛物线y
1=-(x-a
1)
2+a
1与x轴的交点为A
0(0,0),
∴0=-(0-a
1)
2+a
1,解得a
1=1或a
1=0.
由已知a
1>0,∴a
1=1,
∴y
1=-(x-1)
2+1.
令y
1=0,即-(x-1)
2+1=0,解得x=0或x=2,
∴A
1(2,0),b
1=2.
由题意,当n=2时,第2条抛物线y
2=-(x-a
2)
2+a
2经过点A
1(2,0),
∴0=-(2-a
2)
2+a
2,解得a
2=1或a
2=4,
∵a
1=1,且已知a
2>a
1,
∴a
2=4,
∴y
2=-(x-4)
2+4.
∴a
1=1,b
1=2,y
2=-(x-4)
2+4.
(2)抛物线y
2=-(x-4)
2+4,令y
2=0,即-(x-4)
2+4=0,解得x=2或x=6.
∵A
1(2,0),
∴A
2(6,0).
由题意,当n=3时,第3条抛物线y
3=-(x-a
3)
2+a
3经过点A
2(6,0),
∴0=-(6-a
3)
2+a
3,解得a
3=4或a
3=9.
∵a
2=4,且已知a
3>a
2,
∴a
3=9,
∴y
3=-(x-9)
2+9.
∴y
3的顶点坐标为(9,9).
由y
1的顶点坐标(1,1),y
2的顶点坐标(4,4),y
3的顶点坐标(9,9),
依此类推,y
n的顶点坐标为(n
2,n
2).
∵所有抛物线顶点的横坐标等于纵坐标,
∴顶点坐标满足的函数关系式是:y=x.
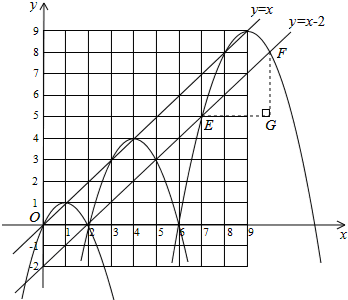
(3)①∵A
0(0,0),A
1(2,0),
∴A
0A
1=2.y
n=-(x-n
2)
2+n
2,令y
n=0,即-(x-n
2)
2+n
2=0,
解得x=n
2+n或x=n
2-n,
∴A
n-1(n
2-n,0),A
n(n
2+n,0),即A
n-1A
n=(n
2+n)-(n
2-n)=2n.
②存在.
设过点(2,0)的直线解析式为y=kx+b,则有:0=2k+b,得b=-2k,
∴y=kx-2k.
设直线y=kx-2k与抛物线y
n=-(x-n
2)
2+n
2交于E(x
1,y
1),F(x
2,y
2)两点,
联立两式得:kx-2k=-(x-n
2)
2+n
2,整理得:x
2+(k-2n
2)x+n
4-n
2-2k=0,
∴x
1+x
2=2n
2-k,x
1•x
2=n
4-n
2-2k.
过点F作FG⊥x轴,过点E作EG⊥FG于点G,则EG=x
2-x
1,
FG=y
2-y
1=[-(x
2-n
2)
2+n
2]-[-(x
1-n
2)
2+n
2]=(x
1+x
2-2n
2)(x
1-x
2)=k(x
2-x
1).
在Rt△EFG中,由勾股定理得:EF
2=EG
2+FG
2,
即:EF
2=(x
2-x
1)
2+[k(x
2-x
1)]
2=(k
2+1)(x
2-x
1)
2=(k
2+1)[(x
1+x
2)
2-4x
1•x
2],
将x
1+x
2=2n
2-k,x
1•x
2=n
4-n
2-2k代入,整理得:EF
2=(k
2+1)[4n
2•(1-k)+k
2+8k],
当k=1时,EF
2=(1+1)(1+8)=18,
∴EF=3
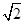
为定值,
∴k=1满足条件,此时直线解析式为y=x-2.
∴存在满足条件的直线,该直线的解析式为y=x-2.
考点: 二次函数综合题.

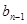 ,0)和An(bn,0).当n=1时,第1条抛物线y1=-(x-a1)2+a1与x轴的交点为A0(0,0)和A1(b1,0),其他依此类推.
,0)和An(bn,0).当n=1时,第1条抛物线y1=-(x-a1)2+a1与x轴的交点为A0(0,0)和A1(b1,0),其他依此类推.

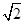 为定值,
为定值,

 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案 应用题作业本系列答案
应用题作业本系列答案 米,在如图所示的坐标系中,这个喷泉的函数关系式是( )
米,在如图所示的坐标系中,这个喷泉的函数关系式是( )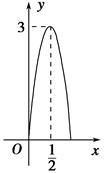
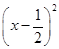 +3
+3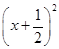 +3
+3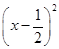 +3
+3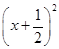 +3
+3 轴,建立平面直角坐标系,点B的坐标为(2,0),若抛物线
轴,建立平面直角坐标系,点B的坐标为(2,0),若抛物线 与扇形OAB的边界总有两个公共点,则实数
与扇形OAB的边界总有两个公共点,则实数 的取值范围是 .
的取值范围是 .