
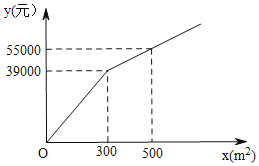
����Ŀ��Ϊ�����������������˾Ӻ�������������һ���㳡����ֲ�ס������ֻ��ܣ����г����飬���ֻ��ܵ���ֲ����y��Ԫ������ֲ���x��m2��֮��ĺ�����ϵ��ͼ��ʾ�����ֻ��ܵ���ֲ����Ϊÿƽ����100Ԫ��
��1����y��x�ĺ�����ϵʽ��
��2���㳡�ϼס������ֻ��ܵ���ֲ�����1000m2�������ֻ��ܵ���ֲ���������200m2���Ҳ��������ֻ�����ֲ�����3������ôӦ����æ����ס������ֻ��ܵ���ֲ�������ʹ��ֲ�������٣������ܷ���Ϊ����Ԫ��
���𰸡���1��![]() ����2��Ӧ�÷���ס������ֻ��ܵ���ֲ����ֱ���750m2 ��250m2������ʹ��ֲ�ܷ������٣������ܷ���Ϊ100000Ԫ��
����2��Ӧ�÷���ס������ֻ��ܵ���ֲ����ֱ���750m2 ��250m2������ʹ��ֲ�ܷ������٣������ܷ���Ϊ100000Ԫ��
��������
��1����ͼ��֪y��x�ĺ�����ϵʽ�Ƿֶκ���������ϵ���������ʽ���ɣ�
��2������ֻ�����ֲΪ am2�������ֻ�����ֲ��1000��a��m2������ʵ���������ȷ��a�ķ�Χ�������ֲ����y��Ԫ������ֲ���x��m2��֮��ĺ�����ϵ���Է����������ٷ���Ϊ���٣�
�⣺��1����0��x��300ʱ����y��k1x�����������300k1��39000�����k1��130����y��130x��
��x��300ʱ����y��k2x+b�����������
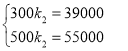 ��
��
���![]() ����y��80x+15000��
����y��80x+15000��
��![]() ��
��
��2������ֻ�����ֲΪ am2�������ֻ�����ֲ��1000��a��m2��
��![]() ��
��
��200��a��750��
��200��a��300ʱ��W��130a+100��1000��a����30a+100000��
��30��0��W��a����������൱a��200 ʱ��Wmin��106000 Ԫ��
��300��a��750ʱ��W��80a+15000+100��1000��a����115000��20a��
�ߩ�20��0��W��a���������С����a��750ʱ��Wmin��100000 Ԫ��
��100000��106000��
�൱a��750ʱ���ܷ������٣������ܷ���Ϊ100000Ԫ��
��ʱ���ֻ�����ֲ���Ϊ1000��750��250m2��
��Ӧ�÷���ס������ֻ��ܵ���ֲ����ֱ���750m2 ��250m2������ʹ��ֲ�ܷ������٣������ܷ���Ϊ100000Ԫ��


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ҹ�Ϊ��ʵ�ֵ�2020��ﵽȫ��С������Ŀ�꣬������Ӵ��˷�ƶ���������ȣ��Ϸ���ij֪����ҵΪ�˰���ijС����ҵ��ƶ��Ͷ��һ�������ÿ���������ɱ�Ϊ18Ԫ�����������з��֣�ÿ��������y(���)�����۵���x(Ԫ)֮��Ĺ�ϵ���Խ��ƿ���һ�κ���y��kx+b����ͳ�Ƶ��ۼ۶�Ϊ30Ԫ/��ʱ��ÿ������40��������ۼ۶�Ϊ35Ԫ/��ʱ��ÿ������30�����
(1)�����k��b��ֵ��
(2)д��ÿ�µ�����w(��Ԫ)�����۵���x(Ԫ)֮��ĺ�������ʽ��
(3)��С����ҵ�ھ�Ӫ�У�ÿ�����۵���ʼ�ձ�����25��x��36Ԫ֮�䣬���С����ҵÿ�»������w(��Ԫ)�ķ�Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������Ȱ���ͼ��ʾ�Ĺ�����һ�������ӡ�������������Ϸ�����������д�����ǣ� ��

A����첻��ʤ�����䣬���Ժ��ʤ�ĸ���Ϊ![]()
B�����ʤ������ʤ�ĸ������
C�����˳���ͬ���Ƶĸ���Ϊ![]()
D������ʤ�ĸ��ʺ����˳���ͬ���Ƶĸ���һ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����������ֽƬABCD�۵���ʹ��DC���ڶԽ���AC�ϣ��ۺ�ΪCE����D�����ڶԽ���D��������AB=3��AD=4����ED�ij�Ϊ

A��![]() B��3 C��1 D��
B��3 C��1 D��![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У�AB=AC����ACΪֱ������O��BC�ڵ�D����AB�ڵ�E������D��DF��AB������ΪF������DE��
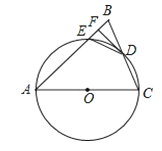
��1����֤��ֱ��DF����O���У�
��2����AE=7��BC=6����AC�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�٣��ھ���ABCD�У�AB��AD���Խ���AC��BD�ཻ�ڵ�O������P�ɵ�A��������AB��BC��CD���D�˶������P���˶�·��Ϊx����AOP�����Ϊy��ͼ����y����x�ĺ�����ϵͼ����AB�ߵij�Ϊ( )
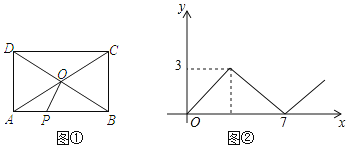
A. 3B. 4C. 5D. 6
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��(1)�Ķ�����
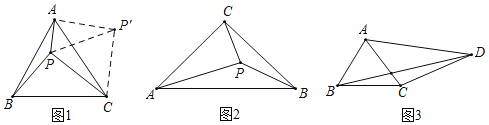
������ת�任�����ѧ������һ�ֳ��õķ�������ͼ1����P�ǵȱ�������ABC��һ�㣬PA��1��PB��![]() ��PC��2�����BPC�Ķ�����
��PC��2�����BPC�Ķ�����
Ϊ������֪�����������ѡ�BPC�Ƶ�C˳ʱ����ת60���á�AP��C������PP������PP���ij�Ϊ_____���ڡ�PAP���У���֤��PAP����90�����ҡ�PP��A�Ķ���Ϊ_____�����Ͽɵá�BPC�Ķ���Ϊ_____��
(2)���Ǩ��
��ͼ2����P�ǵ���Rt��ABC�ڵ�һ�㣬��ACB��90����PA��2��PB��![]() ��PC��1�����APC�Ķ�����
��PC��1�����APC�Ķ�����
(3)��չӦ��
��ͼ3�����ı���ABCD�У�BC��3��CD��5��AB��AC��![]() AD����BAC��2��ADC����ֱ��д��BD�ij���
AD����BAC��2��ADC����ֱ��д��BD�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ı���![]() �У�
��![]() ��
��![]() ��
��![]() ����
����![]() �Ƶ�
�Ƶ�![]() ��ʱ����ת
��ʱ����ת![]() �õ�
�õ�![]() ������
������![]() ������
������![]() ��
��![]() �ڵ�
�ڵ�![]() ����
����![]() �ڵ�
�ڵ�![]() ��
��
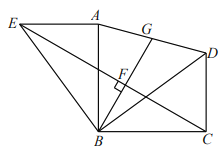
��1����ͼ��![]() ��
��
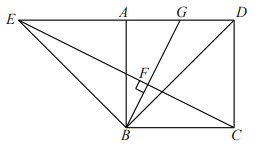
����֤���ı���![]() �������Σ�
��������
����֤��![]() ��
��![]() �е㣻
�е㣻
��2����ͼ����![]() �����ж�
�����ж�![]() �Ƿ���Ȼ��
�Ƿ���Ȼ��![]() ���е㣿���ǣ���֤���������ǣ���˵�����ɣ�
���е㣿���ǣ���֤���������ǣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��![]() ��
��![]() �ֱ��Dz��ȱ�������
�ֱ��Dz��ȱ�������![]() ����
����![]() ���ı�
���ı�![]() ��
��![]() ���е㣮
���е㣮![]() ��
��![]() ƽ���ϵ�һ���㣬����
ƽ���ϵ�һ���㣬����![]() ��
��![]() ��
��![]() ��
��![]() �ֱ���
�ֱ���![]() ��
��![]() ���е㣬˳�����ӵ�
���е㣬˳�����ӵ�![]() ��
��![]() ��
��![]() ��
��![]() ��
��
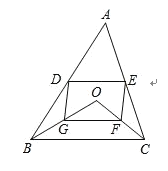
��1����ͼ������![]() ��
��![]() ��ʱ����֤���ı���
��ʱ����֤���ı���![]() ��ƽ���ı��Σ�
��ƽ���ı��Σ�
��2��������![]() ��������
��������![]() ��
��![]() ���ʴ�ʱ�ı���
���ʴ�ʱ�ı���![]() ����ʲô��״������˵�����ɣ�
����ʲô��״������˵�����ɣ�
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com