
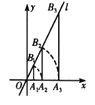
【题目】如图,点![]() 的坐标为
的坐标为![]() ,过点
,过点![]() 作不轴的垂线交直
作不轴的垂线交直![]() 于点
于点![]() 以原点
以原点![]() 为圆心,
为圆心,![]() 的长为半径断弧交
的长为半径断弧交![]() 轴正半轴于点
轴正半轴于点![]() ;再过点
;再过点![]() 作
作![]() 轴的垂线交直线
轴的垂线交直线![]() 于点
于点![]() ,以原点
,以原点![]() 为圆心,以
为圆心,以![]() 的长为半径画弧交
的长为半径画弧交![]() 轴正半轴于点
轴正半轴于点![]() ;…按此作法进行下去,则
;…按此作法进行下去,则![]() 的长是____________.
的长是____________.
科目:初中数学 来源: 题型:
【题目】垫球是排球运动的一项重要技术.下列图表中的数据分别是甲、乙、内三个运动员十次垫球测试的成绩,规则为每次测试连续垫球10个,每垫球到位1个记1分.
测试序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
成绩(分) | 7 | 6 | 8 | 7 | 7 | 5 | 8 | 7 | 8 | 7 |
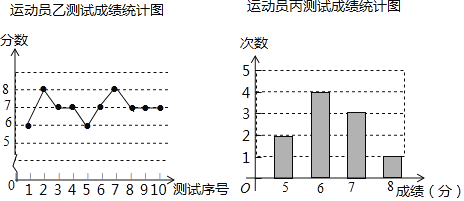
(1)写出运动员甲测试成绩的众数和中位数;
(2)试从平均数和方差两个角度综合分析,若在他们三人中选择一位垫球成绩优秀且较为稳定的接球能手作为自由人,你认为选谁更合适?(参考数据:三人成绩的方差分别为S甲2=0.8、S乙2=0.4、s丙2=0.81)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,点![]() 在数轴上对应的数为
在数轴上对应的数为![]() ,点
,点![]() 对应的数为
对应的数为![]() ,
,![]() 为原点,且
为原点,且![]() 、
、![]() 满足:
满足:![]() .试解答下列问题:
.试解答下列问题:
(1)求数轴上线段![]() 的长度;
的长度;
(2)若点![]() 以每秒2个单位长度的速度沿数轴向右运动,则经过
以每秒2个单位长度的速度沿数轴向右运动,则经过![]() 秒后点
秒后点![]() 表示的数为 ;(用含
表示的数为 ;(用含![]() 的代数式表示)
的代数式表示)
(3)若点![]() ,
,![]() 都以每秒2个单位长度的速度沿数轴向右运动,而点
都以每秒2个单位长度的速度沿数轴向右运动,而点![]() 不动,经过
不动,经过![]() 秒后其中一个点是一条线段的中点,求此时
秒后其中一个点是一条线段的中点,求此时![]() 的值.
的值.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在平行四边形ABCD中,O为对角线BD的中点,过点O的直线EF分别交AD,BC于E,F两点,连结BE,DF.
(1)求证:△DOE≌△BOF.
(2)当∠DOE等于多少度时,四边形BFDE为菱形?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() (
(![]() 为常数),当自变量
为常数),当自变量![]() 的值满足
的值满足![]() 时,与其对应的函数值
时,与其对应的函数值![]() 的最大值为-1,则
的最大值为-1,则![]() 的值为( )
的值为( )
A. 3或6 B. 1或6 C. 1或3 D. 4或6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】新规定:点![]() 为线段
为线段![]() 上一点,当
上一点,当![]() 或
或![]() 时,我们就规定
时,我们就规定![]() 为线段
为线段![]() 的“三倍距点”。如图,在数轴上,点
的“三倍距点”。如图,在数轴上,点![]() 所表示的数为-3,点
所表示的数为-3,点![]() 所表示的数为5.
所表示的数为5.

(1)确定点![]() 所表示的数为___________.
所表示的数为___________.
(2)若动点![]() 从点
从点![]() 出发,沿射线
出发,沿射线![]() 方向以每秒2个单位长度的速度运动,设运动时间为
方向以每秒2个单位长度的速度运动,设运动时间为![]() 秒.
秒.
①当点![]() 与点
与点![]() 重合时,求
重合时,求![]() 的值.
的值.
②求![]() 的长度(用含
的长度(用含![]() 的代数式表示).
的代数式表示).
③当点![]() 为线段
为线段![]() 的“三倍距点”时,直接写出
的“三倍距点”时,直接写出![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正方形![]() ,点
,点![]() 是线段
是线段![]() 延长线上一点,联结
延长线上一点,联结![]() ,其中
,其中![]() .若将
.若将![]() 绕着点
绕着点![]() 逆时针旋转使得
逆时针旋转使得![]() 与
与![]() 第一次重合时,点
第一次重合时,点![]() 落在点
落在点![]() (图中未画出).求:在此过程中,
(图中未画出).求:在此过程中,
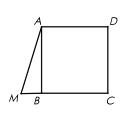
(1)![]() 旋转的角度等于 ______________
旋转的角度等于 ______________![]() .
.
(2)线段![]() 扫过的平面部分的面积为__________(结果保留
扫过的平面部分的面积为__________(结果保留![]() )
)
(3)联结![]() ,则
,则![]() 的面积为____________.
的面积为____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某九年一贯制学校在六年级和九年级的男生中分别随机抽取40名学生测量他们的身高,将数据分组整理后,绘制的频数分布直方图如下:其中两条纵向虚线上端的数值分别是每个年级抽出的40名男生身高的平均数,根据统计图提供的信息,下列结论不合理的是( )
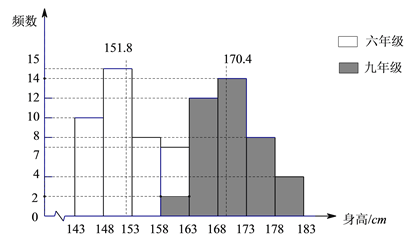
A. 六年级40名男生身高的中位数在第153~158cm组
B. 可以估计该校九年级男生的平均身高比六年级的平均身高高出18.6cm
C. 九年级40名男生身高的中位数在第168~173cm组
D. 可以估计该校九年级身高不低于158cm但低于163cm的男生所占的比例大约是5%
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在正方形ABCD中,P是对角线BD上的点,点E在AB上,且PA=PE.
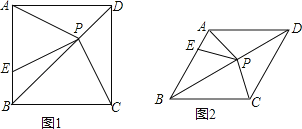
(1)求证:PC=PE;
(2)求∠CPE的度数;
(3)如图2,把正方形ABCD改为菱形ABCD,其他条件不变,试探究∠CPE与∠ABC之间的数量关系,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com