
【题目】某商店经营家居收纳盒,已知成批购进时的单价是20元.调查发现:销售单价是30元时,月销售量是230件,而销售单价每上涨1元,月销售量就减少10件,但每个收纳盒售价不能高于40元.设每个收纳盒的销售单价上涨了![]() 元时(
元时(![]() 为正整数),月销售利润为
为正整数),月销售利润为![]() 元.
元.
(1)求![]() 与
与![]() 的函数关系式.
的函数关系式.
(2)每个收纳盒的售价定为多少元时,月销售利润恰为2520元?
(3)每件玩具的售价定为多少元时可使月销售利润最大?最大的月利润是多少?
科目:初中数学 来源: 题型:
【题目】已知在平面直角坐标系内,抛物线y=x2﹣bx+6经过x轴上两点A,B,点B的坐标为(3,0),与y轴相交于点C.
(1)求抛物线的解析式;
(2)求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】网瘾低龄化已引起社会各界的高度关注,有关部门在全国范围内对12~35岁的网瘾人群进行了随机抽样查,得到了如下两个不定整的统计图,请根据图中信息解答下列问题:
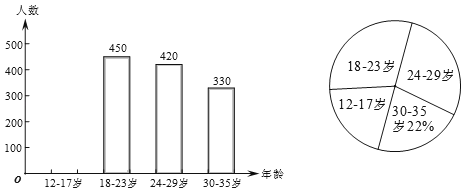
(1)求本次调查了多少名网瘾人员?
(2)通过计算补全条形统计图,在扇形统计图中,18~23岁部分的圆心角的度数为 ;
(3)目前我国12﹣35岁网瘾人数约为3000万,请估计其中12﹣23岁的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程x2﹣(m﹣2)x﹣![]() =0.
=0.
(1)求证:无论m为何值,方程总有两个不相等实数根.
(2)设方程的两实数根为x1,x2,且满足(x1+x2)2=|x1|﹣|x2|+2,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
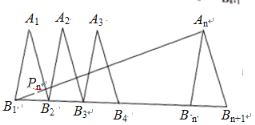
【题目】如图,![]() 个全等的等腰三角形的底边在同一条直线上,底角顶点依次重合.连接第一个三角形的底角顶点
个全等的等腰三角形的底边在同一条直线上,底角顶点依次重合.连接第一个三角形的底角顶点![]() 和第
和第![]() 个三角形的顶角顶点
个三角形的顶角顶点![]() 交
交![]() 于点
于点![]() ,则
,则![]() _________.
_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC和△ADE中,AB=AC,AD=AE,∠BAC+∠EAD=180°,△ABC不动,△ADE绕点A旋转,连接BE,CD,F为BE的中点,连接AF.
(1)如图①,当∠BAE=90°时,求证:CD=2AF;
(2)当∠BAE≠90°时,(1)的结论是否成立?请结合图②说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,点
中,点![]() ,将点A向右平移6个单位长度,得到点B.
,将点A向右平移6个单位长度,得到点B.
(1)直接写出点B的坐标;
(2)若抛物线y=-x2+bx+c经过点A,B,求抛物线的表达式;
(3)若抛物线y=-x2+bx+c的顶点在直线y=x+2上移动,当抛物线与线段AB有且只有一个公共点时,求抛物线顶点横坐标![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,Rt△ABC 中,∠ACB=90°,BC=8,AC=6,点 D 在边 BC 上(不 与点 B、C 重合),点 E 在边 BC 的延长线上,∠DAE=∠BAC,点 F 在线段 AE 上,∠ACF=∠B.设 BD=x.
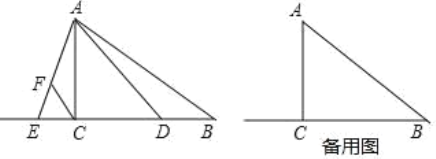
(1)若点 F 恰好是 AE 的中点,求线段 BD 的长;
(2)若 y=![]() ,求 y 关于 x 的函数关系式,并写出它的定义域;
,求 y 关于 x 的函数关系式,并写出它的定义域;
(3)当△ADE 是以 AD 为腰的等腰三角形时,求线段 BD 的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com