

方案一:E→D→A→B;
方案二:E→C→B→A.
经测量得AB=![]() 千米,BC=10千米,CE=6千米,∠BDC=45°,∠ABD=15°.
千米,BC=10千米,CE=6千米,∠BDC=45°,∠ABD=15°.
已知:地下电缆的修建费为2万元/千米,水下电缆的修建费为4万元/千米.
(1)求出河宽AD(结果保留根号);
(2)求出公路CD的长;
(3)哪种方案铺设电缆的费用低?请说明你的理由.
|
思路解析:这是一道几何应用题,解题时要善于把实际问题抽象成几何图形,并领会图形中的几何元素代表的意义,由题意可分析出,当A点距台风中心不超过160千米时,会受台风影响,若过A作AD⊥BC于D,设E,F分别表示A市受台风影响的最初、最后时台风中心的位置,则AE=AF=160千米;当台风中心位于D处时,A市受台风影响的风力最大.
解:(1)如图,经过点A作AD⊥BC,垂足为D. 在Rt△ABD中,AB=220,∠B=30°. 所以AD=110(千米). 由题意,当A点距台风中心不超过160千米时,将会受到台风的影响.故该城市会受到这次台风的影响. (2)由题意,当A点距台风中心不超过160千米时,将会受到台风的影响,由对称性可以知道AE=AF=160千米.当台风中心从E处移到F处时,该城市都会受到这次台风的影响. 在Rt△ADE中,由勾股定理,得
所以EF= 因为该台风中心以15千米/时的速度移动. 所以这次台风影响该城市的持续时间为 (3)当台风中心位于D处时,A市所受这次台风的风力最大,其最大风力为 |


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:初中数学 来源: 题型:
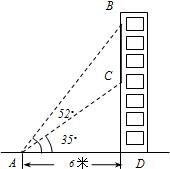 3、如图所示,小华同学在距离某建筑物6米的点A处测得广告牌B点、C点的仰角分别为52°、35°,则广告牌的高度BC为
3、如图所示,小华同学在距离某建筑物6米的点A处测得广告牌B点、C点的仰角分别为52°、35°,则广告牌的高度BC为查看答案和解析>>
科目:初中数学 来源: 题型:
 如图所示,OM是∠AOC的平分线,ON是∠BOC的平分线,
如图所示,OM是∠AOC的平分线,ON是∠BOC的平分线,查看答案和解析>>
科目:初中数学 来源: 题型:
| 月份x(月) | 1 | 2 | 3 | 4 | 5 | … |
| 二氧化碳排放量y(吨) | 48 | 46 | 44 | 42 | 40 | … |

| 51 |
| 52 |
| 53 |
| 54 |
查看答案和解析>>
科目:初中数学 来源: 题型:
.如图所示,OM是∠AOC的平分线,ON是∠BOC的平分线,
(1)如果∠AOC=28°,∠MON=35°,求出∠AOB的度数;
(2)如果∠MON=n°,求出∠AOB的度数;
(3)如果∠MON的大小改变, ∠AOB的大小是否随之改变?它们之间有怎样的大小关系?请写出来.
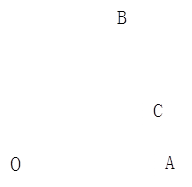 |
![]()
![]()
 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com