
如图,矩形OABC在平面直角坐标系中,O为坐标原点,点A(0,4),C(2,0).将矩形OABC绕点O按顺时针方向旋转135º,得到矩形EFGH(点E与O重合).
(1)若GH交y轴于点M,则∠FOM= ,OM= .
(2)将矩形EFGH沿y轴向上平移t个单位.
①直线GH与x轴交于点D,若AD∥BO,求t的值;
②若矩形EFGH与矩形OABC重叠部分的面积为S个平方单位,试求当0<t≤4 -2时,S与t之间的函数关系式.
-2时,S与t之间的函数关系式.
详见解析.
解析试题分析:(1)由旋转可得出∠AOF=135°,再由矩形的内角为直角得到一个角为直角,利用∠AOF-∠AOC求出∠COF的度数,再由∠MOC为直角,由∠MOC-∠COF即可求出∠MOF的度数;由∠MOF的度数为45°,利用两直线平行得到一对内错角相等,可得出三角形OHM为等腰直角三角形,由OH=MH=2,利用勾股定理即可求出OM的长;
(2)①如图所示,当AD与BO平行时,由AB与DO平行,利用两组对边分别平行的四边形为平行四边形得到ABOD为平行四边形,由平行四边形的对边相等得到AB=DO=2,由平移可知:∠HEM=45°,可得出∠OMD=∠ODM=45°,即三角形ODM为等腰直角三角形,得到OD=OM,由OD的长求出OM的长,由三角形HEM为等腰直角三角形,且直角边长为2,利用勾股定理求出EM的长,用EM-OM即可求出平移的距离,即为t的值;
②分三种情况考虑:(i)如图1所示,当0<t<2时,重叠部分为等腰直角三角形,由平移的距离为t,得到等腰直角三角形直角边为t,利用三角形的面积公式即可表示出S;(ii)如图2所示,当 时,重叠部分为直角梯形,表示出上底,下底及高,利用梯形的面积公式表示出S即可;(iii)如图3所示,当
时,重叠部分为直角梯形,表示出上底,下底及高,利用梯形的面积公式表示出S即可;(iii)如图3所示,当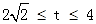
 时,重叠部分为五边形,由梯形面积-三角形面积,表示出S即可.
时,重叠部分为五边形,由梯形面积-三角形面积,表示出S即可.
试题解析:
解:(1)如图所示:
由旋转可得:∠AOF=135°,又∠AOC=90°,
∴∠COF=∠AOF-∠AOC=45°,又∠MOC=90°,
∴∠FOM=45°,又OF∥HG,
∴∠OMH=∠FOM=45°,又∠H=90°,
∴△OHM为等腰直角三角形,
∴OH=HM=2,
则根据勾股定理得: ;
;
(2)①如图所示:连接AD,BO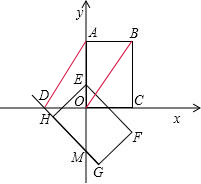
∵AD∥BO,AB∥OD,
∴四边形ADOB为平行四边形,
∴DO=AB=2,
由平移可知:∠HEM=45°,
∴∠OMD=∠ODM=45°,
∴OM=OD=2,由平移可知: ,∴矩形EFGH平移的路程
,∴矩形EFGH平移的路程
 ;
;
②分三种情况考虑:
(i)如图1所示,当0<t≤2时,重叠部分为等腰直角三角形,此时OE=t,则重叠部分面积

(ii)如图2所示,当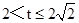 时,重叠部分为直角梯形,
时,重叠部分为直角梯形,
此时

(iii)如图3所示,当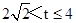
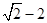 时,E点在A点下方,重叠部分为五边形,此时
时,E点在A点下方,重叠部分为五边形,此时
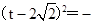


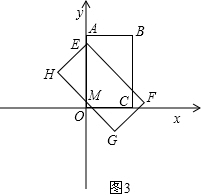
综上, .
.
考点:相似形综合题;矩形的性质;平移的性质;旋转的性质;相似三角形的判定与性质.


 天天练口算系列答案
天天练口算系列答案科目:初中数学 来源: 题型:解答题
如图,已知在矩形ABCD中,AB=2,BC=3,P是线段AD边上的任意一点(不含端点A、D),连结PC,过点P作PE⊥PC交AB于E.
(1)证明△PAE∽△CDP;
(2)当点P在AD上运动时,对应的点E也随之在AB上运动,设AP=x,BE=y,求y与x的函数关系式及y的取值范围;
(3)在线段AD上是否存在不同于P的点Q,使得QC⊥QE?若存在,求线段AP与AQ之间的数量关系;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,在梯形ABCD中,AD∥BC,AD=2,BC=4,点M是AD的中点,△MBC是等边三角形.
(1)求证:梯形ABCD是等腰梯形;
(2)动点P、Q分别在线段BC和MC上运动,且∠MPQ=60°保持不变.设PC=x,MQ=y,求y与x的函数关系式;
(3)在(2)中:
①当动点P、Q运动到何处时,以点P、M和点A、B、C、D中的两个点为顶点的四边形是平行四边形?并指出符合条件的平行四边形的个数;
②当y取最小值时,判断△PQC的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
(已知:如图所示的一张矩形纸片ABCD(AD>AB),将纸片折叠一次,使点A与点C重合,再展开,折痕EF交AD边于点E,交BC边于点F,分别连结AF和CE。
(1)求证:四边形AFCE是菱形;
(2)若AE=10cm,△ABF的面积为24cm2,求△ABF的周长;
(3)在线段AC上是否存在一点P,使得2AE2=AC·AP?若存在,请说明点P的位置,并予以证明;若不存在,请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
已知:如图,在直角梯形ABCD中,AD∥BC,∠B=90°,AD=2,BC=6,AB=3.E为BC边上一点,以BE为边作正方形BEFG,使正方形BEFG和梯形ABCD在BC的同侧.
(1)当正方形的顶点F恰好落在对角线AC上时,求BE的长;
(2)将(1)问中的正方形BEFG沿BC向右平移,记平移中的正方形BEFG为正方形B′EFG,当点E与点C重合时停止平移.设平移的距离为t,正方形B′EFG的边EF与AC交于点M,连接B′D,B′M,DM.是否存在这样的t,使△B′DM是直角三角形?若存在,求出t的值;若不存在,请说明理由;
(3)在(2)问的平移过程中,设正方形B′EFG与△ADC重叠部分的面积为S,请直接写出S与t之间的函数关系式以及自变量t的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图:已知一次函数 的图像分别交
的图像分别交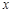 轴、
轴、 轴于
轴于 、
、 两点,且点
两点,且点 在一次函数
在一次函数 的图像上,
的图像上, ⊥
⊥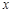 轴于点
轴于点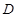 .
.
(1)求 的值及
的值及 、
、 两点的坐标;
两点的坐标;
(2)如果点 在线段
在线段 上,且
上,且 ,求
,求 点的坐标;
点的坐标;
(3)如果点 在
在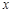 轴上,那么当△
轴上,那么当△ 与△
与△ 相似时,求点
相似时,求点 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
已知在△ABC中,∠ABC=90°,AB=3,BC=4.点Q是线段AC上的一个动点,过点Q作AC的垂线交线段AB(如图1)或线段AB的延长线(如图2)于点P.
(1)当点P在线段AB上时,求证:△APQ∽△ABC;
(2)当△PQB为等腰三角形时,求AP的长.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,在△ABC中,∠C=90°,AC+BC=9,点O是斜边AB上一点,以O为圆心2为半径的圆分别与AC、BC相切于点D、E。
(1)求AC、BC的长;
(2)若AC=3,连接BD,求图中阴影部分的面积(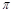 取3.14)。
取3.14)。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com