
【题目】如图,四边形ABCD中,AB=BC=2CD,AB∥CD,∠C=90°,E是BC的中点,AE与BD相交于点F,连接DE.

(1)求证:△ABE≌△BCD;
(2)判断线段AE与BD的数量关系及位置关系,并说明理由;
(3)若CD=1,试求△AED的面积.
【答案】(1)见解析;(2)AE=BD,AE⊥BD,理由见解析;(3)△AED的面积为![]() .
.
【解析】
(1)由已知条件可推导得到![]() ,由SAS即可证明△ABE≌△BCD;
,由SAS即可证明△ABE≌△BCD;
(2)由(1)可得△ABE≌△BCD 可得AE=BD,再由角的转化可得∠AFB=90°,即可证明AE⊥BD;
(3)因为 △AED的面积=梯形ABCD的面积﹣△ABE的面积﹣△CDE的面积,即可求解△AED的面积.
(1)证明:∵AB∥CD,
∴∠ABE+∠C=180°,
∵∠C=90°,
∴∠ABE=90°=∠C,
∵E是BC的中点,
∴BC=2BE,
∵BC=2CD,
∴BE=CD,
在△ABE和△BCD中, ,
,
∴△ABE≌△BCD(SAS);
(2)解:AE=BD,AE⊥BD,理由如下:
由(1)得:△ABE≌△BCD,
∴AE=BD,
∵∠BAE=∠CBD,∠ABF+∠CBD=90°,
∴∠ABF+∠BAE=90°,
∴∠AFB=90°,
∴AE⊥BD;
(3)解:∵△ABE≌△BCD,
∴BE=CD=1,
∵AB=BC=2CD=2,
∴CE=BC﹣BE=1,
∴CE=CD,
∴△AED的面积=梯形ABCD的面积﹣△ABE的面积﹣△CDE的面积=![]() (1+2)×2﹣
(1+2)×2﹣![]() ×2×1﹣
×2×1﹣![]() ×1×1=
×1×1=![]()


科目:初中数学 来源: 题型:
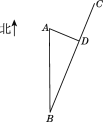
【题目】如图,某沿海城市A接到台风警报,在该城市正南方向260 km的B处有一台风中心,沿BC方向以15 km/h的速度向C移动,已知城市A到BC的距离AD=100 km,那么台风中心经过多长时间从B点移动到D点?如果在距台风中心30 km的圆形区域内都将受到台风的影响,正在D点休息的游人在接到台风警报后的几小时内撤离才可以免受台风的影响?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在正方形ABCD中,AC是对角线,今有较大的直角三角板,一边始终经过点B,直角顶点P在射线AC上移动,另一边交DC于点Q.
(1)如图①,当点Q在DC边上时,猜想并写出PB与PQ所满足的数量关系,并加以证明;
(2)如图②,当点Q落在DC的延长线上时,猜想并写出PB与PQ满足的数量关系,并证明你的猜想.

查看答案和解析>>
科目:初中数学 来源: 题型:
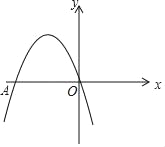
【题目】如图,二次函数y=ax2﹣4x+c的图象经过坐标原点,与x轴交于点A(﹣4,0)
(1)求此二次函数的解析式,并求出抛物线的顶点坐标;
(2)在抛物线上存在点P,使△AOP的面积为10?求出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校有![]() 名学生,为了解全校学生的上学方式,该校数学兴趣小组在全校随机抽取了
名学生,为了解全校学生的上学方式,该校数学兴趣小组在全校随机抽取了![]() 名学生进行抽样调查,整理样本数据,得到下列图表(频数分布表中部分划记被污染渍盖住):
名学生进行抽样调查,整理样本数据,得到下列图表(频数分布表中部分划记被污染渍盖住):
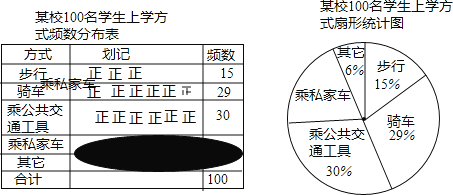
(1)![]() ;
;
(2)求扇形统计图中,乘私家车部分对应的圆心角的度数;
(3)请估计该校![]() 名学生中,选择骑车和步行上学的一共有多少人?
名学生中,选择骑车和步行上学的一共有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
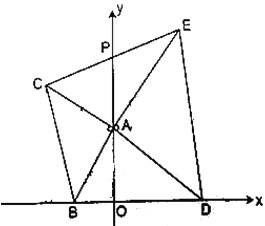
【题目】平面直角坐标系![]() 中,
中,![]() ,
,![]() 分别在
分别在![]() 轴正半轴和
轴正半轴和![]() 轴负半轴上,
轴负半轴上,![]() 在第二象限,满足:
在第二象限,满足:![]() ,
,![]() .已知
.已知![]() .
.
(1)求![]() ,
,![]() 的坐标;
的坐标;
(2)求点![]() 的坐标及
的坐标及![]() 的面积;
的面积;
(3)已知![]() 是
是![]() 轴的正半轴上一点,
轴的正半轴上一点,![]() ,
,![]() 在第一象限,
在第一象限,![]() ,
,![]() ,连接
,连接![]() 交
交![]() 轴于点
轴于点![]() .
.
①求证:![]() .
.
②在点![]() 的移动过程中,给出以下两个结论:(i)
的移动过程中,给出以下两个结论:(i)![]() 的值不变;(ii)
的值不变;(ii)![]() 的值不变,其中有且只有一个是正确的,请你找出这个结论并求其值.
的值不变,其中有且只有一个是正确的,请你找出这个结论并求其值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在Rt△ACB中,∠ACB=90°,AC=3,BC=4,有一过点C的动圆⊙O与斜边AB相切于动点P,连接CP.
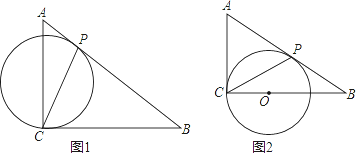
(1)当⊙O与直角边AC相切时,如图2所示,求此时⊙O的半径r的长;
(2)随着切点P的位置不同,弦CP的长也会发生变化,试求出弦CP的长的取值范围.
(3)当切点P在何处时,⊙O的半径r有最大值?试求出这个最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】本学期实验中学组织开展课外兴趣活动,各活动小班根据实际情况确定了计划组班人数,并发动学生自愿报名,报名人数与计划人数的前5位情况如下:
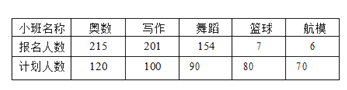
若用同一小班的计划人数与报名人数的比值大小来衡量进入该班的难易程度,学生中对于进入各活动小班的难易有以下预测:①篮球和航模都能进;②舞蹈比写作容易;③写作比奥数容易;④舞蹈比奥数容易.则预测正确的有___________(填序号即可).
查看答案和解析>>
科目:初中数学 来源: 题型:
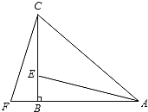
【题目】如图,在△ABC中,AB=CB,∠BAC=∠BCA,∠ABC=90°,F为AB延长线上一点,点E在BC上,且AE=CF.
(1)求证:Rt△ABE≌ Rt△CBF;
(2)求证:AE⊥CF;
(3)若∠CAE=30°,求∠ACF度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com