
 如图,抛物线y=ax2+bx-3,顶点为E,该抛物线与x轴交于A,B两点,与y轴交于点C,且OB=OC=3OA.直线$y=-\frac{1}{3}x+1$与y轴交于点D.求∠DBC-∠CBE.
如图,抛物线y=ax2+bx-3,顶点为E,该抛物线与x轴交于A,B两点,与y轴交于点C,且OB=OC=3OA.直线$y=-\frac{1}{3}x+1$与y轴交于点D.求∠DBC-∠CBE. 分析 先求出点D、点C的坐标,得出点B、A的坐标,求出抛物线的解析式,得出抛物线的顶点坐标,根据勾股定理求出BC、CE、BE,由勾股定理的逆定理证明△BCE为直角三角形,∠BCE=90°,由三角函数证出∠DBO=∠CBE,即可得出∠DBC-∠CBE=∠DBC-∠DBO=∠OBC=45°.
解答 解:将x=0代入y=$-\frac{1}{3}x+1$,y=1,
∴D(0,1),
将x=0代入y=ax2+bx-3得:y=-3,
∴C(0,-3),
∵OB=OC=3OA,
∴B(3,0),A(-1,0),∠OBC=45°,
对于直线y=$-\frac{1}{3}x+1$,
当y=0时,x=3,
∴直线y=$-\frac{1}{3}x+1$过点B.
将点C(0,-3)的坐标代入y=a(x+1)(x-3),
得:a=1,
∴抛物线的解析式为:y=x2-2x-3=(x-1)2-4,
∴抛物线y=x2-2x-3的顶点为E(1,-4).
于是由勾股定理得:
BC=$3\sqrt{2}$,CE=$\sqrt{2}$,BE=$2\sqrt{5}$.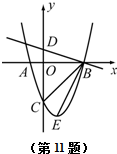 ∵BC2+CE2=BE2,
∵BC2+CE2=BE2,
∴△BCE为直角三角形,∠BCE=90°,
因此tan∠CBE=$\frac{CE}{CB}$=$\frac{1}{3}$.
又tan∠DBO=$\frac{OD}{OB}=\frac{1}{3}$,
则∠DBO=∠CBE,
∴∠DBC-∠CBE=∠DBC-∠DBO=∠OBC=45°.
点评 本题考查了坐标与图形性质、抛物线与坐标轴的交点坐标、抛物线的解析式的求法及顶点坐标、勾股定理、勾股定理的逆定理、三角函数;本题综合性强,有一定难度.


科目:初中数学 来源: 题型:解答题
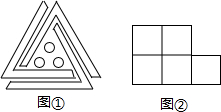 (1)图①是轴对称图形吗?如果是,它有几条对称轴?如果不是,可以怎样把它补成轴对称图形?
(1)图①是轴对称图形吗?如果是,它有几条对称轴?如果不是,可以怎样把它补成轴对称图形?查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
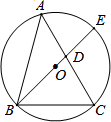 定义:对于任意的三角形,设其三个内角的度数分别为x°、y°和z°,若满足x2+y2=z2,则称这个三角形为勾股三角形.
定义:对于任意的三角形,设其三个内角的度数分别为x°、y°和z°,若满足x2+y2=z2,则称这个三角形为勾股三角形.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com