
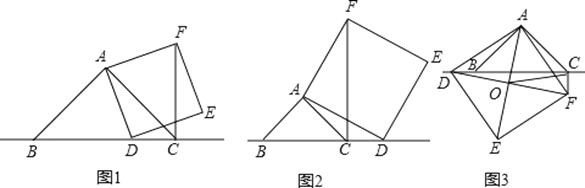
【题目】已知,在△ABC中,∠BAC=90°,∠ABC=45°,点D为直线BC上一动点(点D不与点B,C重合).以AD为边作正方形ADEF,连接CF.
(1)如图1,当点D在线段BC上时.求证:CF+CD=BC;
(2)如图2,当点D在线段BC的延长线上时,其他条件不变,请直接写出CF,BC,CD三条线段之间的关系;
(3)如图3,当点D在线段BC的反向延长线上时,且点A,F分别在直线BC的两侧,其他条件不变;
①请直接写出CF,BC,CD三条线段之间的关系;
②若正方形ADEF的边长为2![]() ,对角线AE,DF相交于点O,连接OC.求OC的长度.
,对角线AE,DF相交于点O,连接OC.求OC的长度.
【答案】(1)证明见解析;(2)CF-CD=BC;(3)①CD-CF=BC;②2.
【解析】试题分析:(1)、根据正方形的性质判定出△BAD和△CAF全等,从而得出BD=CF,根据BD+CD=BC得出答案;(2)、根据图形得出线段之间的关系;(3)、首先根据正方形的性质证明△BAD和△CAF全等,然后得出∠ACF=∠ABD=135°,从而说明△FCD为直角三角形,根据正方形的对角线得出DF的长度,然后根据直角三角形斜边上的中线的性质得出OC的长度.
试题解析:(1)、∵∠BAC=90°,∠ABC=45°,∴∠ACB=∠ABC=45°,∴AB=AC,
∵四边形ADEF是正方形,∴AD=AF,∠DAF=90°,
∵∠BAD=90°-∠DAC,∠CAF=90°-∠DAC,∴∠BAD=∠CAF,
则在△BAD和△CAF中,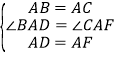 ∴△BAD ≌ △CAF(SAS),∴BD=CF,
∴△BAD ≌ △CAF(SAS),∴BD=CF,
∵BD+CD=BC,∴CF+CD=BC;
(2)、CF-CD=BC
(3)、①CD-CF =BC.
②∵∠BAC=90°,∠ABC=45°,∴∠ACB=∠ABC=45°,∴AB=AC, ∵四边形ADEF是正方形,
∴AD=AF,∠DAF=90°, ∵∠BAD=90°-∠BAF,∠CAF=90°-∠BAF,∴∠BAD=∠CAF,
则在△BAD和△CAF中,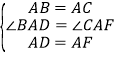 ∴△BAD ≌ △CAF(SAS),
∴△BAD ≌ △CAF(SAS),
∴∠ABD=∠ACF,∵∠ABC=45°,∠ABD=135°, ∴∠ACF=∠ABD=135°,
∴∠FCD=90°,∴△FCD是直角三角形. ∵正方形ADEF的边长为![]() 且对角线AE、DF相交于点O,
且对角线AE、DF相交于点O,
∴DF=![]() AD=4,O为DF中点. ∴OC=
AD=4,O为DF中点. ∴OC=![]() DF=2.
DF=2.


科目:初中数学 来源: 题型:
【题目】一项工程,甲、乙两公司合做,12天可以完成,共需付工费102000元;如果甲、乙两公司单独完成此项公程,乙公司所用时间是甲公司的1.5倍,乙公司每天的施工费比甲公司每天的施工费少1500元。
(1)甲、乙公司单独完成此项工程,各需多少天?
(2)若让一个公司单独完成这项工程,哪个公司施工费较少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题14分)如图①,已知抛物线![]() (a≠0)与
(a≠0)与![]() 轴交于点A(1,0)和点B(-3,0),与y轴交于点C.
轴交于点A(1,0)和点B(-3,0),与y轴交于点C.

(1)求抛物线的解析式;
(2)设抛物线的对称轴与![]() 轴交于点M,问在对称轴上是否存在点P,使△CMP为等腰三角形?若存在,请直接写出所有符合条件的点P的坐标;若不存在,请说明理由.
轴交于点M,问在对称轴上是否存在点P,使△CMP为等腰三角形?若存在,请直接写出所有符合条件的点P的坐标;若不存在,请说明理由.
(3)如图②,若点E为第二象限抛物线上一动点,连接BE、CE,求四边形BOCE面积的最大值,并求此时E点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在学校组织的社会实践活动中,甲、乙两人参加了射击比赛,每人射击七次,命中的环数如表:
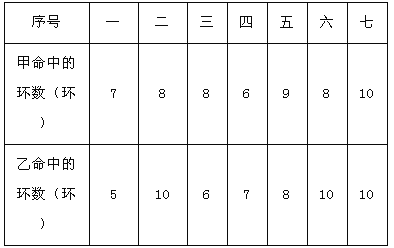
根据以上信息,解决以下问题:
(1)写出甲、乙两人命中环数的众数;
(2)已知通过计算器求得![]() =8,
=8,![]() ≈1.43,试比较甲、乙两人谁的成绩更稳定?
≈1.43,试比较甲、乙两人谁的成绩更稳定?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com