
如图,PQ为圆O的直径,点B在线段PQ的延长线上,OQ=QB=1,动点A在圆O的上半圆运动(含P、Q两点),以线段AB为边向上作等边三角形ABC.
(1)当线段AB所在的直线与圆O相切时,求△ABC的面积(图1);
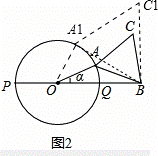
(2)设∠AOB=α,当线段AB、与圆O只有一个公共点(即A点)时,求α的范围(图2,直接写出答案);
(3)当线段AB与圆O有两个公共点A、M时,如果AO⊥PM于点N,求CM的长度(图3).
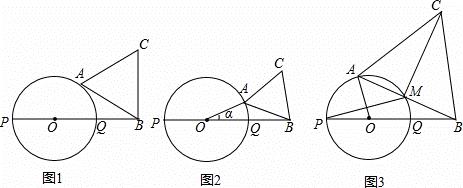
解:(1)连接OA,过点B作BH⊥AC,垂足为H,如图1所示.
∵AB与⊙O相切于点A,
∴OA⊥AB.
∴∠OAB=90°.
∵OQ=QB=1,
∴OA=1.
∴AB=
=
=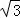 .
.
∵△ABC是等边三角形,
∴AC=AB=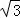 ,∠CAB=60°.
,∠CAB=60°.
∵sin∠HAB= ,
,
∴HB=AB•sin∠HAB
=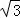 ×
×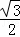
=.
∴S△ABC=AC•BH
=× ×
×
= .
.
∴△ABC的面积为 .
.
(2)①当点A与点Q重合时,
线段AB与圆O只有一个公共点,此时α=0°;
②当线段A1B所在的直线与圆O相切时,如图2所示,
线段A1B与圆O只有一个公共点,
此时OA1⊥BA1,OA1=1,OB=2,
∴cos∠A1OB= =.
=.
∴∠A1OB=60°.
∴当线段AB与圆O只有一个公共点(即A点)时,
α的范围为:0°≤α≤60°.
(3)连接MQ,如图3所示.
∵PQ是⊙O的直径,
∴∠PMQ=90°.
∵OA⊥PM,
∴∠PDO=90°.
∴∠PDO=∠PMQ.
∴△PDO∽△PMQ.
∴ =
= =
=
∵PO=OQ=PQ.
∴PD=PM,OD=MQ.
同理:MQ=AO,BM=AB.
∵AO=1,
∴MQ=.
∴OD=.
∵∠PDO=90°,PO=1,OD=,
∴PD= .
.
∴PM=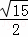 .
.
∴DM= .
.
∵∠ADM=90°,AD=A0﹣OD=,
∴AM=
=
=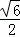 .
.
∵△ABC是等边三角形,
∴AC=AB=BC,∠CAB=60°.
∵BM=AB,
∴AM=BM.
∴CM⊥AB.
∵AM=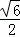 ,
,
∴BM= ,AB=
,AB=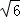 .
.
∴AC=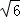 .
.
∴CM=
=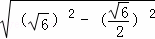
=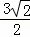 .
.
∴CM的长度为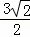 .
.




科目:初中数学 来源: 题型:
为了鼓励居民节约用水,某市采用“阶梯水价”的方法按月计算每户家庭的水费:每月用水量不超过20吨时,按每吨2元计费;每月用水量超过20吨时,其中的20吨仍按每吨2元计费,超过部分按每吨2.8元计费,设每户家庭每月用水量为x吨时,应交水费y元.
(1)分别求出0≤x≤20和x>20时,y与x之间的函数表达式;
(2)小颖家四月份、五月份分别交水费45.6元、38元,问小颖家五月份比四月份节约用水多少吨?
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,直线a∥b,△ABC是等边三角形,点A在直线a上,边BC在直线b上,把△ABC沿BC方向平移BC的一半得到△A′B′C′(如图①);继续以上的平移得到图②,再继续以上的平移得到图③,…;请问在第100个图形中等边三角形的个数是 .

查看答案和解析>>
科目:初中数学 来源: 题型:
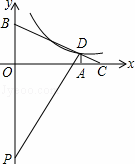
如图,在平面直角坐标系中,Rt△PBD的斜边PB落在y轴上,tan∠BPD=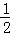 .延长BD交x轴于点C,过点D作DA⊥x轴,垂足为A,OA=4,OB=3.
.延长BD交x轴于点C,过点D作DA⊥x轴,垂足为A,OA=4,OB=3.
(1)求点C的坐标;
(2)若点D在反比例函数y=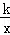 (k>0)的图象上,求反比例函数的解析式.
(k>0)的图象上,求反比例函数的解析式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com