Question

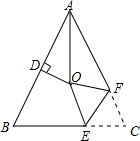
14．如图，△ABC中，AB=AC，∠BAC的平分线与AB的垂直平分线交于点O，将∠C沿EF（E在BC上，F在AC上）折叠，点C与点O恰好重合．若∠OEC=136°，则∠BAC的大小为（　　）

• A． 44°
• B． 58°
• C． 64°
• D． 68°

Answer 1

分析 如图连接OB、OC．首先证明OB=OA=OC，设∠OBA=∠OAB=∠OAC=∠OCA=x，求出∠OCB=∠OBC=22°，根据三角形内角和定理列出方程即可解决问题．

解答 解：如图连接OB、OC．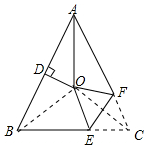

在△AOB和△AOC中，
$\left\{\begin{array}{l}{AO=AO}\\{∠OAB=∠OAC}\\{AB=AC}\end{array}\right.$，
∴△AOB≌△AOC，
∴OB=OC，
∵OD垂直平分AB，
∴OA=OB=OC，
∴∠OBA=∠OAB=∠OAC=∠OCA，设∠OBA=∠OAB=∠OAC=∠OCA=x．
∵∵∠OEC=136°，EO=EC，
∴∠EOC=∠ECO=$\frac{1}{2}$（180°-∠OEC）=22°，
∴∠OBC=∠OCE=22°，
∵∠ABC+∠ACB+∠BAC=180°，
∴4x+2×22°=180°，
∴x=34°，
∴∠BAC=2x=68°，
故选D．

点评 本题考查翻折变换、线段垂直平分线的性质、等腰三角形的性质和判定、三角形内角和定理等知识，解题的关键是灵活运用所学知识解决问题，学会添加常用辅助线，构造特殊三角形解决问题，属于中考常考题型．