
如图,已知在△ABC中,AB=AC,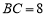 ,
,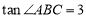 ,AD⊥BC于D,O是AD上一点,OD=3,以OB为半径的⊙O分别交AB、AC于E、F.
,AD⊥BC于D,O是AD上一点,OD=3,以OB为半径的⊙O分别交AB、AC于E、F.
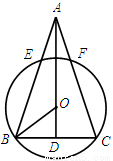
求:(1)⊙O的半径;
(2)BE的长.
(1)⊙O的半径是5;(2)BE的长是
【解析】
试题分析:
(1)根据等腰三角形性质求出BD,根据勾股定理求出OB即可;
(2)根据垂径定理得出BH=HE,证三角形AHO和三角形ADB相似,得出比例式,求出AH,求出AB,求出BH即可.
试题解析:
【解析】
(1)∵AB=AC,AD⊥BC,BC=8,
∴BD=CD=4,
在RT△BOD中∵OD=3,
∴由勾股定理得:OB=5;
(2)过O点作OH⊥AB,交AB于H,
又∵OH过圆心O,
∴BH=EH,
∵在RT△ABD中,tan∠ABD= =3,
=3,
∴AD=12,由勾股定理得:AB= ,
,
∵OD=3,
∴AO=9,
∵∠OAH=∠BAD,∠OHA=∠ADB,
∵△AOH∽△ABD,
∴
∴
∴
∴
∴
考点:相似三角形的判定与性质;等腰三角形的性质;垂径定理;解直角三角形.


科目:初中数学 来源:2013-2014学年中考数学章节复习测试全等三角形练习卷(解析版) 题型:选择题
使两个直角三角形全等的条件是
A.两条边对应相等 B.一条边对应相等
C.两锐角对应相等 D.一锐角对应相等
查看答案和解析>>
科目:初中数学 来源:2013-2014学年上海市浦东新区中考二模数学试卷(解析版) 题型:解答题
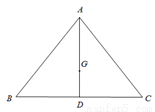
如图,已知在△ABC中,AB=AC,BC比AB大3,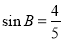 ,点G是△ABC的重心,AG的延长线交边BC于点D.过点G的直线分别交边AB于点P、交射线AC于点Q.
,点G是△ABC的重心,AG的延长线交边BC于点D.过点G的直线分别交边AB于点P、交射线AC于点Q.
(1)求AG的长;
(2)当∠APQ=90º时,直线PG与边BC相交于点M.求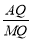 的值;
的值;
(3)当点Q在边AC上时,设BP=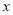 ,AQ=
,AQ=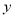 ,求
,求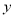 关于
关于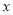 的函数解析式,并写出它的定义域.[
的函数解析式,并写出它的定义域.[
查看答案和解析>>
科目:初中数学 来源:2013-2014学年上海市毕业生学业模拟考试数学试卷(解析版) 题型:填空题
一公路大桥引桥长100米,已知引桥的坡度 ,那么引桥的铅直高度为 米(结果保留根号).
,那么引桥的铅直高度为 米(结果保留根号).
查看答案和解析>>
科目:初中数学 来源:2013-2014学年上海市松江区中考二模数学试卷(解析版) 题型:填空题
如果三角形有一边上的中线长恰好等于这边的长,那么称这个三角形为“有趣三角形”,这条中线称为“有趣中线”.已知Rt△ABC中,∠B=90°,较短的一条直角边边长为1,如果Rt△ABC是“有趣三角形”,那么这个三角形“有趣中线”长等于
查看答案和解析>>
科目:初中数学 来源:2013-2014学年上海市杨浦区5月中考二模数学试卷(解析版) 题型:选择题
点A是数轴上的任意一点,则下列说法正确的是( )
A.点A表示的数一定是整数
B.点A表示的数一定是分数
C.点A表示的数一定是有理数
D.点A表示的数可能是无理数
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com