
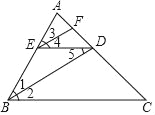
【题目】在△ABC中,AB=AC,∠BAC=50° ,D是BC的中点,以AC为腰向外作等腰直角△ACE,∠EAC=90°,连接BE,交AD于点F,交AC于点G.
(1)求∠AEB的度数;
(2)求证:∠AEB=∠ACF;
(3)若AB=4,求![]() 的值.
的值.

【答案】(1)20°;(2)32.
【解析】
(1)根据等腰直角三角形的旋转得出∠ABE=∠AEB,求出∠BAE,根据三角形内角和定理求出即可;
(2)根据等腰三角形的性质得出∠BAF=∠CAF,根据SAS推出△BAF≌△CAF,根据全等得出∠ABF=∠ACF,即可得出答案;
(3)根据全等得出BF=CF,求出∠CFG=∠EAG=90°,根据勾股定理求出EF2+BF2=EF2+CF2=EC2,EC2=AC2+AE2,即可得出答案.
(1)∵AB=AC,AC=AE.
∴AB=AE,
∴∠AEB=∠ABE.
∵∠BAC=50°,∠CAE=90°,
∴∠BAE=50°+90°=140°.
∴∠AEB=![]() .
.
(2)∵AB=AC,D是BC的中点,
∴∠BAF=∠CAF.
∴△ABF≌△ACF.
∴∠ABF=∠ACF.
∵∠AEB=∠ABE,
∴∠AEB=∠ACF.
(3)∵∠AEB=∠ACF ,∠AGE=∠CGF,
∴∠CFE=∠CAE=90°.
∴![]() .
.
∵CF=BF,
∴![]() .
.
∵![]() ,
,
∴![]() .
.


 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案科目:初中数学 来源: 题型:
【题目】中学生带手机上学的现象越来越受到社会的关注,为此,某记者随机调查了某城区若干名学生家长对这种现象的态度(态度分为:A:无所谓;B:基本赞成;C:赞成;D:反对),并将调查结果绘制成频数折线图1和统计图2(不完整)。请根据图中提供的信息,解答下列问题:
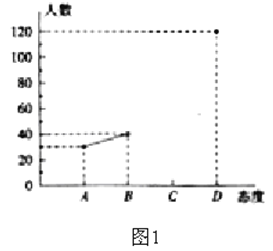
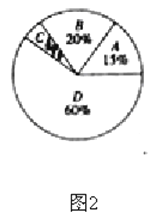
(1)此次抽样检查中,共调查了 名学生家长;
(2)将图1补充完整;
(3)根据抽样检查的结果,请你估计该市城区6000名中学生家长中有多少名家长持反对态度?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 如图,△ABC是等边三角形,P是三角形内一点,PD∥AB,PE∥BC,PF∥AC,若△ABC的周长为18,则PD+PE+PF=( )
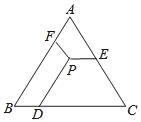
A. 18B. 9![]()
C. 6D. 条件不够,不能确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线y=ax2+bx+c(a≠0)与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,点A的坐标为(﹣1,0),且OC=OB,tan∠ACO= ![]() .
.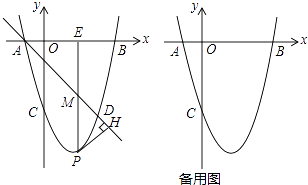
(1)求抛物线的解析式;
(2)若点D和点C关于抛物线的对称轴对称,直线AD下方的抛物线上有一点P,过点P作PH⊥AD于点H,作PM平行于y轴交直线AD于点M,交x轴于点E,求△PHM的周长的最大值;
(3)在(2)的条件下,以点E为端点,在直线EP的右侧作一条射线与抛物线交于点N,使得∠NEP为锐角,在线段EB上是否存在点G,使得以E,N,G为顶点的三角形与△AOC相似?如果存在,请求出点G的坐标;如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,BD是∠ABC的平分线,ED∥BC,∠4=∠5,则EF也是∠AED的平分线.完成下列推理过程:
证明:∵BD是∠ABC的平分线(已知)
∴∠1=∠2(角平分线定义)
∵ED∥BC(已知)
∴∠5=∠2( )
∴∠1=∠5(等量代换)
∵∠4=∠5(已知)
∴EF∥ ( )
∴∠3=∠1( )
∴∠3=∠4(等量代换)
∴EF是∠AED的平分线(角平分线定义)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】以x为自变量的二次函数y=x2﹣2(b﹣2)x+b2﹣1的图象不经过第三象限,则实数b的取值范围是( )
A.b≥ ![]()
B.b≥1或b≤﹣1
C.b≥2
D.1≤b≤2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,BC为半圆的直径,O为圆心,D是弧AC的中点,四边形ABCD的对角线AC,BD交于点E,BC= ![]() ,CD=
,CD= ![]() ,则sin∠AEB的值为 .
,则sin∠AEB的值为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于实数a,我们规定:用符号![]() 表示不大于
表示不大于![]() 的最大整数,称
的最大整数,称![]() 为a的根整数,例如:
为a的根整数,例如:![]() ,
,![]() =3.
=3.
(1)仿照以上方法计算:![]() =______;
=______;![]() =_____.
=_____.
(2)若![]() ,写出满足题意的x的整数值______.
,写出满足题意的x的整数值______.
如果我们对a连续求根整数,直到结果为1为止.例如:对10连续求根整数2次![]()
![]()
![]() =1,这时候结果为1.
=1,这时候结果为1.
(3)对100连续求根整数,____次之后结果为1.
(4)只需进行3次连续求根整数运算后结果为1的所有正整数中,最大的是____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=1,BC=2,BC在x轴上,一次函数y=kx﹣2的图象经过点A、C,并与y轴交于点E,反比例函数y= ![]() 的图象经过点A.
的图象经过点A.
(1)点E的坐标是;
(2)求反比例函数的解析式;
(3)求当一次函数的值小于反比例函数的值时,x的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com