
【题目】在数学活动课上,老师提出了一个问题:把一副三角尺如图摆放,直角三角尺的两条直角边分别垂直或平行,60°角的顶点在另一个三角尺的斜边上移动,在这个运动过程中,有哪些变量,能研究它们之间的关系吗?
小林选择了其中一对变量,根据学习函数的经验,对它们之间的关系进行了探究.
下面是小林的探究过程,请补充完整:
(1)画出几何图形,明确条件和探究对象;
如图2,在Rt△ABC中,∠C=90°,AC=BC=6cm,D是线段AB上一动点,射线DE⊥BC于点E,∠EDF=60°,射线DF与射线AC交于点F.设B,E两点间的距离为xcm,E,F两点间的距离为ycm.
(2)通过取点、画图、测量,得到了x与y的几组值,如下表:
x/cm | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
y/cm | 6.9 | 5.3 | 4.0 | 3.3 | 4.5 | 6 |
(说明:补全表格时相关数据保留一位小数)
(3)建立平面直角坐标系,描出以补全后的表中各对对应值为坐标的点,画出该函数的图象;
(4)结合画出的函数图象,解决问题:当△DEF为等边三角形时,BE的长度约为 cm.
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】阅读下列材料,并完成相应任务.
 古希腊数学家,天文学家欧多克索斯(Eudoxus,约前400—前347)曾提出:能否将一
古希腊数学家,天文学家欧多克索斯(Eudoxus,约前400—前347)曾提出:能否将一
条线段分成不相等的两部分.使较短线段与较长线段的比等于较长线段与原线段的比,这个相等的比就是![]() ,黄金分割在我们生活中有广泛运用.黄金分割点也可以用折纸的方式得到.
,黄金分割在我们生活中有广泛运用.黄金分割点也可以用折纸的方式得到.
第一步:裁一张正方形的纸片![]() ,先折出
,先折出![]() 的中点
的中点![]() ,然后展平,再折出线段
,然后展平,再折出线段![]() ,再展平;
,再展平;
第二步:将纸片沿![]() 折叠,使
折叠,使![]() 落到线段
落到线段![]() 上,
上,![]() 的对应点为
的对应点为![]() ,展平;
,展平;
第三步:沿![]() 折叠,使
折叠,使![]() 落在
落在![]() 上,
上,![]() 的对应点为
的对应点为![]() ,展平,这时
,展平,这时![]() 就是
就是![]() 的黄金分割点.
的黄金分割点.

 古希腊数学家,天文学家欧多克索斯(Eudoxus,约前400—前347)曾提出:能否将一
古希腊数学家,天文学家欧多克索斯(Eudoxus,约前400—前347)曾提出:能否将一
条线段分成不相等的两部分.使较短线段与较长线段的比等于较长线段与原线段的比,这个相等的比就是![]() ,黄金分割在我们生活中有广泛运用.黄金分割点也可以用折纸的方式得到.
,黄金分割在我们生活中有广泛运用.黄金分割点也可以用折纸的方式得到.
第一步:裁一张正方形的纸片![]() ,先折出
,先折出![]() 的中点
的中点![]() ,然后展平,再折出线段
,然后展平,再折出线段![]() ,再展平;
,再展平;
第二步:将纸片沿![]() 落到线段
落到线段![]() 上,
上,![]() 的对应点为
的对应点为![]() ,展平;
,展平;
第三步:沿![]() 折叠,使
折叠,使![]() 落在
落在![]() 上,
上,![]() 的对应点为
的对应点为![]() ,展平,这时
,展平,这时![]() 就是
就是![]() 的黄金分割点.
的黄金分割点.

任务:(1)试根据以上操作步骤证明![]() 就是
就是![]() 的黄金分割点;
的黄金分割点;
(2)请写出一个生活中应用黄金分割的实际例子.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC,∠BAC=α,点P是△ABC内一点,且![]() .连接PB,试探究PA,PB,PC满足的等量关系.
.连接PB,试探究PA,PB,PC满足的等量关系.
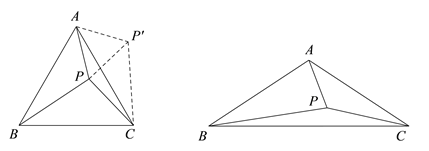
图1 图2
(1)当α=60°时,将△ABP绕点A逆时针旋转60°得到![]() ,连接
,连接![]() ,如图1所示.
,如图1所示.
由![]() ≌
≌![]() 可以证得
可以证得![]() 是等边三角形,再由
是等边三角形,再由![]() 可得∠APC的大小为 度,进而得到
可得∠APC的大小为 度,进而得到![]() 是直角三角形,这样可以得到PA,PB,PC满足的等量关系为 ;
是直角三角形,这样可以得到PA,PB,PC满足的等量关系为 ;
(2)如图2,当α=120°时,请参考(1)中的方法,探究PA,PB,PC满足的等量关系,并给出证明;
(3)PA,PB,PC满足的等量关系为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知正多边形每个内角比相邻外角大60°.
(1)求这个正多边形的边数;
(2)求这个正多边形的内切圆与外切圆的半径之比;
(3)将这个多边形对折,并完全重合,求得到图形的内角和是多少度(按一层计算)?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2018年我国科技实力进一步增强,嫦娥探月、北斗组网、航母海试、鲲龙击水、港珠澳大桥正式通车……,这些成就的取得离不开国家对科技研发的大力投入.下图是2014年—2018年我国研究与试验发展(R&D)经费支出及其增长速度情况. 2018年我国研究与试验发展(R&D)经费支出为19657亿元,比上年增长11.6%,其中基础研究经费1118亿元.
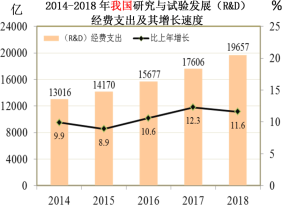
根据统计图提供的信息,下列说法中合理的是( )
A. 2014年—2018年,我国研究与试验发展(R&D)经费支出的增长速度始终在增加
B. 2014年—2018年,我国研究与试验发展(R&D)经费支出增长速度最快的年份是2017年
C. 2014年—2018年,我国研究与试验发展(R&D)经费支出增长最多的年份是2017年
D. 2018年,基础研究经费约占该年研究与试验发展( (R&D)经费支出的10%
查看答案和解析>>
科目:初中数学 来源: 题型:
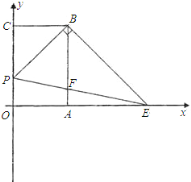
【题目】如图,已知矩形OABC,以点O为坐标原点建立平面直角坐标系,其中A(2,0),C(0,3),点P以每秒1个单位的速度从点C出发在射线CO上运动,连接BP,作BE⊥PB交x轴于点E,连接PE交AB于点F,设运动时间为t秒.在运动的过程中,写出以P、O、E为顶点的三角形与△ABE相似时t的值为_____________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() (其中m>0)与x轴交于A、B两点(A在B的左侧),与y轴交于点C,连接AC、BC
(其中m>0)与x轴交于A、B两点(A在B的左侧),与y轴交于点C,连接AC、BC
(1)直接写出点A、点C的坐标;
(2)当∠ACB=90°时,点D是第一象限抛物线上一动点,连接OD,当OD的长最小时,求点D的坐标;
(3)直线![]() 经过点B,与抛物线交于另一点G,点P在y轴上,点Q在抛物线上,以点B、G、P、Q为顶点的四边形能否为矩形?若能,求出点P的坐标,若不能,请说明理由.
经过点B,与抛物线交于另一点G,点P在y轴上,点Q在抛物线上,以点B、G、P、Q为顶点的四边形能否为矩形?若能,求出点P的坐标,若不能,请说明理由.
(4) 当tan∠CBO=![]() 时,动点P从点A出发,以每秒2个单位长度的速度沿射线AO方向匀速运动,动点Q从点B出发,以每秒1个单位长度的速度沿射线BO方向匀速运动,P、Q两点同时运动,相遇时停止,在运动过程中,以PQ为一边在x轴上方作正方形PQMN,设运动时间为t秒.不妨设正方形PQMN和△ABC重叠部分的面积为S,请直接写出S关于t的函数表达式.
时,动点P从点A出发,以每秒2个单位长度的速度沿射线AO方向匀速运动,动点Q从点B出发,以每秒1个单位长度的速度沿射线BO方向匀速运动,P、Q两点同时运动,相遇时停止,在运动过程中,以PQ为一边在x轴上方作正方形PQMN,设运动时间为t秒.不妨设正方形PQMN和△ABC重叠部分的面积为S,请直接写出S关于t的函数表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,D是BC的中点,过D点的直线GF交AC于F,交AC的平行线BG于G点,DE⊥DF,交AB于点E,连结EG、EF.

(1)求证:BG=CF.
(2)请你判断BE+CF与EF的大小关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A1,A2,A3,… 和B1,B2,B3,… 分别在直线![]() 和x轴上.△OA1 B1,△B1 A2 B2,△B2 A3 B3,…都是等腰直角三角形.如果点A1(1,1),那么点A2019的纵坐标是( )
和x轴上.△OA1 B1,△B1 A2 B2,△B2 A3 B3,…都是等腰直角三角形.如果点A1(1,1),那么点A2019的纵坐标是( )
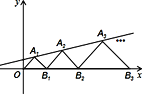
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com