
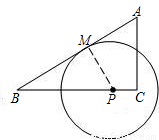
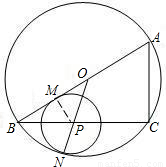
 (1)证明:∵AB切⊙P于点M,
(1)证明:∵AB切⊙P于点M,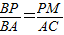 ,
,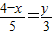 ,
,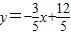 (0≤x<4).
(0≤x<4).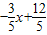 ,
, ,
, <x<4时,⊙P与AC所在的直线相离.
<x<4时,⊙P与AC所在的直线相离.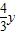 ,
,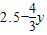 ,
,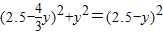 ,
,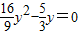
 .
. 时,x=
时,x=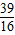 .
.

 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案科目:初中数学 来源:2009年浙江省温州市永嘉县中考数学二模试卷(解析版) 题型:解答题
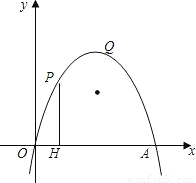
查看答案和解析>>
科目:初中数学 来源:2009年浙江省温州市永嘉县中考数学二模试卷(解析版) 题型:解答题
| 款式 | 成本(元/个) | 售价(元/个) |
| A | 2 | 2.3 |
| B | 3 | 3.5 |
查看答案和解析>>
科目:初中数学 来源:2009年福建省三明市大田二中自主招生数学模拟试卷(3)(解析版) 题型:解答题
查看答案和解析>>
科目:初中数学 来源:2006年某重点中学理科试点班招生数学试卷(浙教版)(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com