
����Ŀ����ͼ������OAB������ƽ��ֱ������ϵxOy�У���OAB=90����OA=2��AB=![]() ������OAB��x��ĸ�����ƽ��2OA�ij��Ⱥ�õ���DCE��
������OAB��x��ĸ�����ƽ��2OA�ij��Ⱥ�õ���DCE��
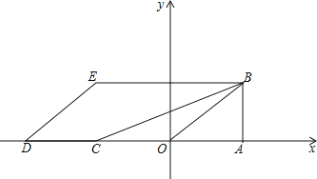
��1������ԭ���������y=ax2+bx+c������B��E����������ߵĽ���ʽ��
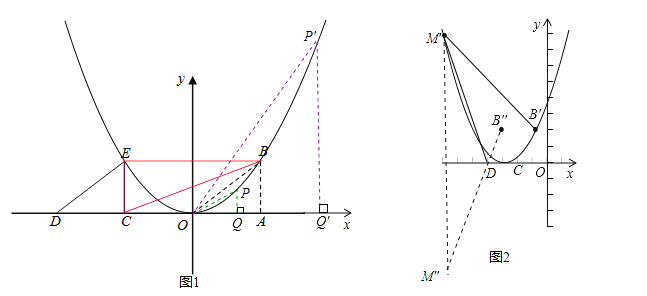
��2������P�ڸ����������ƶ�������p�ڵ�һ������ʱ������p��PQ��x���ڵ�Q������OP������O��P��QΪ���������������B��C��EΪ��������������ƣ�ֱ��д����P�����ꣻ
��3������M����4��n���ڸ��������ϣ�ƽ�������ߣ���ƽ�ƺ��M�Ķ�Ӧ��ΪM������B�Ķ�Ӧ��ΪB���������������������ƽ��ʱ���Ƿ����ij��λ�ã�ʹ�ı���M��B��CD���ܳ���̣������ڣ������ʱ�����ߵĽ���ʽ���������ڣ���˵�����ɣ�
���𰸡���1��y=![]() x2����2��P��1��
x2����2��P��1��![]() ����P ��
����P ��![]() ��
��![]() ������3�����ڣ�������������ƽ��
������3�����ڣ�������������ƽ��![]() ����λʱ���ı���M��B��CD���ܳ���̣���ʱ�����ߵĽ���ʽΪy=
����λʱ���ı���M��B��CD���ܳ���̣���ʱ�����ߵĽ���ʽΪy=![]() ��x+
��x+![]() ��2��
��2��
��������
�����������1������ƽ�Ƶ��������B��E�����꣬Ȼ�����ô���ϵ����������ú����Ľ���ʽ����2����P���������Ϊ��x��![]() ������Ϊ��BEC=��OQP=90����������O��P��QΪ���������������B��C��EΪ���������������ʱ��Q��Eһ����Ӧ��Ȼ�����������������ۣ���i����OQP�ס�BEC����ii����PQO�ס�BEC���������������ζ�Ӧ�߳ɱ����г�����ʽ����⼴�ɣ���3������ƽ��ʱ��ʹM'D+CB'��̼��ɣ���ô������M������x��ԳƵ������ΪM�����õ�ֱ��B��M���Ľ���ʽ����y=0�������Ӧ�ĵ�����ꣻ�����õ������߶���ƽ�ƵĹ��ɣ��ö���ʽ�����Ӧ�ĺ�������ʽ�����¶���������뼴��.
������Ϊ��BEC=��OQP=90����������O��P��QΪ���������������B��C��EΪ���������������ʱ��Q��Eһ����Ӧ��Ȼ�����������������ۣ���i����OQP�ס�BEC����ii����PQO�ס�BEC���������������ζ�Ӧ�߳ɱ����г�����ʽ����⼴�ɣ���3������ƽ��ʱ��ʹM'D+CB'��̼��ɣ���ô������M������x��ԳƵ������ΪM�����õ�ֱ��B��M���Ľ���ʽ����y=0�������Ӧ�ĵ�����ꣻ�����õ������߶���ƽ�ƵĹ��ɣ��ö���ʽ�����Ӧ�ĺ�������ʽ�����¶���������뼴��.
�����������1��������ã�B��2��![]() ������OC=2��CE=
������OC=2��CE=![]() ����E����2��
����E����2��![]() ����
����
�������߾���ԭ��͵�B��E�����������ߵĽ���ʽΪy=ax2��a��0����
�������߾�����B��2��![]() ������
������![]() =4a����ã�a=
=4a����ã�a=![]() ��
��
�������ߵĽ���ʽΪy=![]() x2��
x2��
��2������P���������ϣ������P������Ϊ��x��![]() x2����
x2����
�������������i������OQP�ס�BECʱ����![]() ����
���� 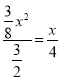 ����ã�x=1������P������Ϊ��1��
����ã�x=1������P������Ϊ��1��![]() ����
����
��ii������PQO�ס�BECʱ����![]() ����
����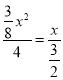 ����ã�x=
����ã�x=![]() ������P������Ϊ��
������P��������![]() ��
��![]() ����
����
�������������������ĵ�P��������P��1��![]() ����P ��
����P ��![]() ��
��![]() ����
����
��3�����ڣ�
��Ϊ�߶�M��B����CD�ij��Ƕ�ֵ������Ҫʹ�ı���M��B��CD���ܳ���̣�ֻҪʹM��D+CB����̣�
���������������ƽ�ƣ���Ȼ��M��D+CB����MD+CB����˲�����ij��λ�ã�ʹ�ı���M��B��CD���ܳ���̣���ȻӦ�ý������� y=![]() x2����ƽ�ƣ�
x2����ƽ�ƣ�
����֪M����4��6����������������ƽ����n����λ�����M����B��������ֱ�Ϊ
M������4��n��6����B����2��n��![]() ����
����
��ΪCD=2����˽���B������ƽ��2����λ��B������n��![]() ����
����
ҪʹM��D+CB����̣�ֻҪʹM��D+DB����̣���M������x��ԳƵ������ΪM������4��n����6����
��ֱ��M��B���Ľ���ʽy=kx+b��k��0������DӦ��ֱ��M��B���ϣ�
��ֱ��M��B���Ľ���ʽΪy=![]() ����B������n��
����B������n��![]() �����룬���n=
�����룬���n=![]() ��
��
�ʽ�����������ƽ��![]() ����λʱ���ı���M��B��CD���ܳ���̣���ʱ�����ߵĽ���ʽΪy=
����λʱ���ı���M��B��CD���ܳ���̣���ʱ�����ߵĽ���ʽΪy=![]() ��x+
��x+![]() ��2��
��2��


 ����ȫ���ִʾ��ƪ��ϵ�д�
����ȫ���ִʾ��ƪ��ϵ�д� �����߿����ϵ�д�
�����߿����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ѷֱ��������2��3��4��5���ĸ�С�����A�����ѷֱ��������![]() ��
�� ![]() ��
�� ![]() ������С�����B��������С�����״����С���ʵؾ���ͬ��A��B�������Ӳ�����
������С�����B��������С�����״����С���ʵؾ���ͬ��A��B�������Ӳ�����
��1�������A����������С���ϵ�����Ϊ3���ٴ�B��������һ��С������С���ϵ����ֻ�Ϊ�����ĸ����� ��
��2��С���ֱ��A��B���������и�����һ��С��������״ͼ���б����г����п��ܳ��ֵĽ��������������С���ϵ����ֻ�Ϊ�����ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪ABΪ��O��ֱ����PΪ��O������һ�㣬���P����AB�ĶԳƵ�P�����O��λ�ù�ϵΪ�� ��
A. ��P���ڡ�O�� B. ��P���ڡ�O��
C. ��P���ڡ�O�� D. ����ȷ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijͬѧ����ij�ֹ���д������һ�����֣�122 122 122 122 122����,��д����93������ʱ��1���ֵ�Ƶ���ǣ� ����
A. 33 B. 32 C. 31 D. 30
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڵ���ʽ3xy,x2y,y3�У�����дһ������ʽ��ʹһ�ε���ʽ���ֵ�Ƶ��Ϊ25�� ��_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
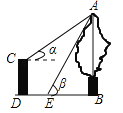
����Ŀ����ͼ��CD��һ��Ϊ4��ƽ̨��AB����CD�ײ���ƽ��һ��������ƽ̨��C��������A������Ǧ�=30�㣬��ƽ̨�ײ������ķ���ˮƽǰ��3�����E���ڵ�E���������A������Ǧ�=60�㣬������AB������������ţ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
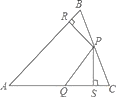
����Ŀ����ͼ����ABC�У�P��Q�ֱ���BC��AC�ϵĵ㣬��PR��AB��PS��AC������ֱ���R��S����AQ=PQ��PR=PS,AB=AC�������������ۣ���AS=AR����PQ��AB���ۡ�BRP�ա�CSP��������ȷ���ǣ�������
A. �٢� B. �ڢ� C. �٢� D. �٢ڢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC �У���O��AC���ϵ�һ�����㣬����O��ֱ��MN��BC����MN����BCA�Ľ�ƽ�����ڵ�E������BCA����ǡ�ACGƽ�����ڵ�F��
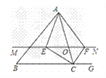
��1����˵��EO=FO��
��2������O�˶����δ�ʱ���ı���AECF�Ǿ��Σ���˵�����ɣ�
��3������O�˶����δ����ҡ�ABC����ʲô����ʱ���ı���AECF �������Σ���˵�����ɣ�
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com