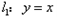练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    如图，直线与双曲线相交于点A（a，2），将直线l1向上平移3个单位得到l2，直线l2与双曲线相交于B．C两点（点B在第一象限），交y轴于D点．
    （1）求双曲线的解析式；
    （2）求tan∠DOB的值
    解：（1）∵A（a，2）是y=x与y=的交点，
    ∴A（2，2），
    把A（2，2）代入y=，得k=4，
    ∴双曲线的解析式为y=；
    （2）∵将l1向上平移了3个单位得到l2，
    ∴l2的解析式为y=x+3，
    ∴解方程组，
    得，，
    ∴B （1，4），
    ∴tan∠DOB=
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    如图，P是双曲线y=
    4x
    (x＞0)    的一个分支上的一点，以点P为圆心，1个单位长度为半径作⊙P，设点P的坐标为（x，y）．
    （1）求当x为何值时，⊙P与直线y=3相切，并求点P的坐标．
    （2）直接写出当x为何值时，⊙P与直线y=3相交、相离．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    （本题10分）如图，P是双曲线的一个分支上的一点，以点P为圆心，1个单位长度为半径作⊙P，设点P的坐标为（，）．
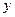    （1）求当为何值时，⊙P与直线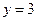相切，并求点P的坐标．
    （2）直接写出当为何值时，⊙P与直线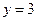相交、相离．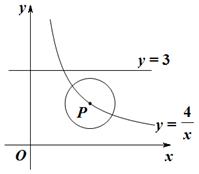

    查看答案和解析>>

    科目：初中数学 来源：2011-2012学年江苏省海安县曲塘中学附属初级中学九年级上学期期中考试数学卷 题型：解答题

    （本题10分）如图，P是双曲线的一个分支上的一点，以点P为圆心，1个单位长度为半径作⊙P，设点P的坐标为（，）．
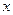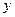    （1）求当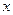为何值时，⊙P与直线相切，并求点P的坐标．
    （2）直接写出当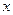为何值时，⊙P与直线相交、相离．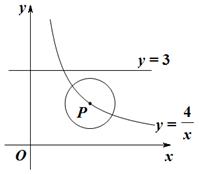

    查看答案和解析>>

    科目：初中数学 来源：2012届海安县曲塘中学附属中学初三第一学期数学卷 题型：解答题

    如图，P是双曲线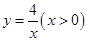的一个分支上的一点，以点P为圆心，1个单位长度为半径作⊙P，设点P的坐标为（，）．

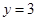    1.求当为何值时，⊙P与直线相切，并求点P的坐标．

    2.直接写出当为何值时，⊙P与直线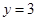相交、相离．

     

    查看答案和解析>>

    科目：初中数学 来源：2012届江苏省附属初级中学九年级上学期期中考试数学卷 题型：解答题

    （本题10分）如图，P是双曲线的一个分支上的一点，以点P为圆心，1个单位长度为半径作⊙P，设点P的坐标为（，）．

    （1）求当为何值时，⊙P与直线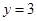相切，并求点P的坐标．

    （2）直接写出当为何值时，⊙P与直线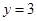相交、相离．

     

     

    查看答案和解析>>

    同步练习册答案