
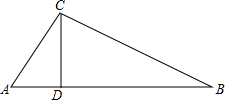
 如图,在△ABC中,∠ACB=90°,过点C作CD⊥AB于D,AC=3cm,BC=4cm,AB=5cm.
如图,在△ABC中,∠ACB=90°,过点C作CD⊥AB于D,AC=3cm,BC=4cm,AB=5cm.分析 (1)由于在△ABC中,根据勾股定理的逆定理得到∠ACB=90°,CD⊥AB,故图中的所有直角三角形有Rt△ADC、Rt△BDC、Rt△ACB;
(2)根据直角三角形的面积计算CD的长.
解答 解:(1)∵AC=3cm,BC=4cm,AB=5cm,
∴AC2+BC2=32+42=52=AB2,
∴∠ACB=90°,
∵CD⊥AB,
∴直角三角形有:Rt△ADC、Rt△BDC、Rt△ACB;
(2)∵S△ABC=$\frac{1}{2}$AB•CD=$\frac{1}{2}$AC•BC
∴5CD=3×4
∴CD=2.4cm
∴△ABC的面积是6cm2.
点评 本题考查的是勾股定理的逆定理,直角三角形的性质及其面积公式


 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案科目:初中数学 来源: 题型:选择题
 点C是线段AB上一点,点M是AC的中点,点N是BC的中点,如果MC比NC长2cm,AC比BC长( )
点C是线段AB上一点,点M是AC的中点,点N是BC的中点,如果MC比NC长2cm,AC比BC长( )| A. | 1 cm | B. | 2 cm | C. | 4 cm | D. | 6 cm |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 小王购买了一套经济适用房,他准备将地面铺上地砖,地面结构如图所示,根据图中的数据(单位:m),解答下列问题:
小王购买了一套经济适用房,他准备将地面铺上地砖,地面结构如图所示,根据图中的数据(单位:m),解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
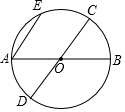 已知:如图,AB,CD是⊙O的直径,AE是⊙O的弦,若AE∥CD,求证:$\widehat{AD}$=$\widehat{BC}$=$\widehat{EC}$.
已知:如图,AB,CD是⊙O的直径,AE是⊙O的弦,若AE∥CD,求证:$\widehat{AD}$=$\widehat{BC}$=$\widehat{EC}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com