
【题目】若x﹣y=8,xy=10,则x2+y2=________
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】已知一个数a的近似值为1.50,那么数a的准确值的范围是( )
A. 1.495<a<1.505 B. 1 .495≤a<1.505 C. 1.45≤a<1.55 D. 1.45<a<1.55
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题背景
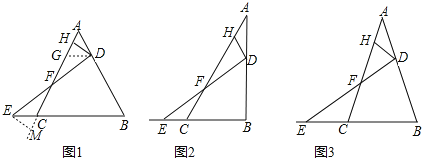
已知在△ABC中,AB边上的动点D由A向B运动(与A、B不重合),点E与点D同时出发,由点C沿BC的延长线方向运动(E不与C重合),连接DE交AC于点F,点H是线段AF上一点.
(1)初步尝试
如图1,若△ABC是等边三角形,DH⊥AC,且点D,E的运动速度相等.求证:HF=AH+CF.
小王同学发现可以由以下两种思路解决问题:
思路一:过点D作DG∥BC,交AC于点G,先证GH=AH,再证GF=CF,从而证得结论成立;
思路二:过点E作EM⊥AC,交AC的延长线于点M,先证CM=AH,再证HF=MF,从而证得结论成立.
请你任选一种思路,完整地书写本小题的证明过程(如用两种方法作答,则以第一种方法评分);
(2)类比探究
如图2,若在△ABC中,∠ABC=90°,∠ADH=∠BAC=30°,且点D,E的运动速度之比是![]() :1,求
:1,求![]() 的值;
的值;
(3)延伸拓展
如图3,若在△ABC中,AB=AC,∠ADH=∠BAC=36°,记![]() =m,且点D,E的运动速度相等,试用含m的代数式表示
=m,且点D,E的运动速度相等,试用含m的代数式表示![]() (直接写出结果,不必写解答过程).
(直接写出结果,不必写解答过程).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,函数y=kx+b和函数y=ax+m的图象,求下列不等式(组)的解集

(1)kx+b<0的解集是 ;
(2)ax+m≥0的解集是 ;
(3)kx+b<ax+m的解集是 ;
(4)ax+m>kx+b>0的解集是 ;
(5)0<ax+m<kx+b的解集是 。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列调查中,适合普查的事件是( )
A. 调查华为手机的使用寿命v
B. 调查市九年级学生的心理健康情况
C. 调查你班学生打网络游戏的情况
D. 调查中央电视台《中国舆论场》的节目收视率
查看答案和解析>>
科目:初中数学 来源: 题型:
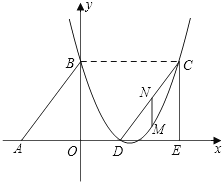
【题目】如图,Rt△ABO的两直角边OA、OB分别在x轴的负半轴和y轴的正半轴上,O为坐标原点,A、B两点的坐标分别为(﹣3,0)、(0,4),抛物线y=![]() +bx+c经过B点,且顶点在直线x=
+bx+c经过B点,且顶点在直线x=![]() 上.
上.
(1)求抛物线对应的函数关系式;
(2)若△DCE是由△ABO沿x轴向右平移得到的,当四边形ABCD是菱形时,试判断点C和点D是否在该抛物线上,并说明理由;
(3)在(2)的前提下,若M点是CD所在直线下方该抛物线上的一个动点,过点M作MN平行于y轴交CD于点N.设点M的横坐标为t,MN的长度为l.求l与t之间的函数关系式,并求l取最大值时,点M的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com