
【题目】如图,⊙O是锐角△ABC的外接圆,FH是⊙O的切线,切点为F,FH∥BC,连结AF交BC于E,∠ABC的平分线BD交AF于D,连结BF.下列结论:①AF平分∠BAC;②点F为△BDC的外心;③![]() ;④若点M,N分别是AB和AF上的动点,则BN+MN的最小值是ABsin∠BAC.其中一定正确的是_____(把你认为正确结论的序号都填上).
;④若点M,N分别是AB和AF上的动点,则BN+MN的最小值是ABsin∠BAC.其中一定正确的是_____(把你认为正确结论的序号都填上).
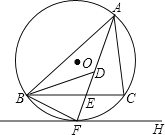
【答案】①②③④
【解析】
如图1,连接OF,CF,通过切线的性质证OF⊥FH,进而由FH∥BC,得OF⊥BC,即可由垂径定理得到F是弧BC的中点,根据圆周角定理可得∠BAF=∠CAF,可得AF平分∠BAC;由三角形外角性质和同弧所对的圆周角相等可得∠BDF=∠FBD,可得BF=DF=CF,可得点F为△BDC的外心;如图2,过点C作CG∥AB,交AF的延长线于点G,通过证明△BAE∽△CGE,可得![]() ,即可判断③;如图3,作点M关于AF的对称点M',当点N在线段BM'上,且BM'⊥AC时,BN+MN有最小值为BM',即可判断④.
,即可判断③;如图3,作点M关于AF的对称点M',当点N在线段BM'上,且BM'⊥AC时,BN+MN有最小值为BM',即可判断④.
解:如图1,连接OF,CF,
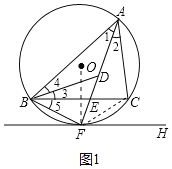
∵FH是⊙O的切线,
∴OF⊥FH,
∵FH∥BC,
∴OF⊥BC,且OF为半径,
∴OF垂直平分BC,
∴![]() =
=![]() ,
,
∴∠1=∠2,BF=CF,
∴AF平分∠BAC,故①正确,
∵∠1=∠2,∠4=∠3,∠5=∠2,
∴∠1+∠4=∠2+∠3,
∴∠1+∠4=∠5+∠3,
∵∠1+∠4=∠BDF,∠5+∠3=∠FBD,
∴∠BDF=∠FBD,
∴BF=FD,且BF=CF,
∴BF=DF=CF,
∴点F为△BDC的外心,故②正确;
如图2,过点C作CG∥AB,交AF的延长线于点G,
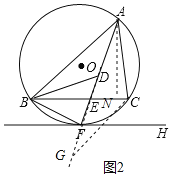
∵CG∥AB,
∴∠BAE=∠EGC,且∠BAE=∠CAE,
∴∠CAE=∠CGE,
∴AC=CG,
∵CG∥AB,
∴△BAE∽△CGE,
∴![]() ,
,
∴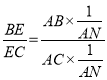 =
=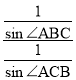 =
=![]() ,
,
故③正确;
如图3,作点M关于AF的对称点M',

∵点M与点M'关于AF对称,
∴MN=M'N,
∴BN+MN=BN+M'N,
∴当点N在线段BM'上,且BM'⊥AC时,BN+MN有最小值为BM',且sin∠BAC=![]() ,
,
∴BN+MN最小值为ABsin∠BAC,
故④正确,
故答案为:①②③④.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
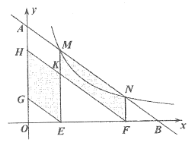
【题目】如图,直线![]() 与反比例函数
与反比例函数![]() 的图像交于点
的图像交于点![]() 、
、![]() ,与
,与![]() 轴、
轴、![]() 轴分别交于点
轴分别交于点![]() 、
、![]() ,作
,作![]() 轴于点
轴于点![]() ,
,![]() 轴于点
轴于点![]() ,过点
,过点![]() 、
、![]() 分别作
分别作![]() ,
,![]() ,分别交
,分别交![]() 轴于点
轴于点![]() 、
、![]() ,
,![]() 交
交![]() 于点
于点![]() ,若四边形
,若四边形![]() 和四边形
和四边形![]() 的面积和为12,则
的面积和为12,则![]() 的值为_______.
的值为_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于x的一元二次方程x2+(2k+1)x+k2+1=0有两个不等实根x1、x2.
(1)求实数k的取值范围.
(2)若方程两实根x1、x2满足x1+x2=﹣x1x2,求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“泥兴陶,,是钦州的一张文化名片。钦州市某妮兴陶公司以每只60元的价格销售一种成本价为40元的文化纪念杯,每星期可售出100只。后来经过市场调查发现,每只杯子的售价每降低1元,则平均何星期可多买出10只。若该公司销售这种文化纪念杯要想平均每星期获利2240元,请回答:
(1)每只杯应降价多少元?
(2)在平均每星期获利不变的情况下,为尽可能让利于顾客,赢得市场,该公司应该按原售价的几折出售?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:
小红遇到这样一个问题:如图1,在四边形ABCD中,∠A=∠C=90°,∠D=60°,AB=![]() ,BC=
,BC=![]() ,求AD的长.
,求AD的长.
小红发现,延长AB与DC相交于点E,通过构造Rt△ADE,经过推理和计算能够使问题得到解决(如图2).
请回答:AD的长为 .
参考小红思考问题的方法,解决问题:
如图3,在四边形ABCD中,tanA=![]() ,∠B=∠C=135°,AB=9,CD=3,求BC和AD的长.
,∠B=∠C=135°,AB=9,CD=3,求BC和AD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在锐角△ABC中,∠A、∠B、∠C的对边分别是a、b、c,其外接圆的半径为r.
(探究)
(1)如图甲,作直径BD,若r=3,发现![]() 的值为 .
的值为 .
(2)猜想![]() ,
,![]() ,
,![]() 之间的关系,并证明你的猜想.
之间的关系,并证明你的猜想.

(应用)
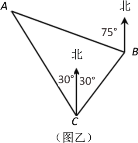
(3)如图乙,一货轮在C处测得灯塔A在货轮的北偏西30°的方向上,随后货轮以60海里/时的速度按北偏东30°的方向航行,半小时后到达B处,此时又测得灯塔A在货轮的北偏西75°的方向上,求此时货轮距灯塔A的距离AB.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点![]() 在双曲线上,
在双曲线上,![]() 垂直
垂直![]() 轴,垂足为
轴,垂足为![]() ,点
,点![]() 在
在![]() 上,
上,![]() 平行于
平行于![]() 轴交双曲线于点
轴交双曲线于点![]() ,直线
,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,已知
,已知![]()
![]() ,点
,点![]() 的坐标为
的坐标为![]() .
.
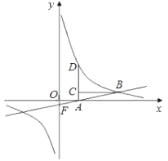
(1)求反比例函数和一次函数的表达式;
(2)直接写出反比例函数值大于一次函数值时自变量的值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线的顶点坐标是(1,4),且过点(2,5),
(1)求抛物线的函数表达式;
(2)求将抛物线向左平移几个单位,可以使平移后的抛物线经过原点?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com