
���� ��1������AAS֤����ABE�ա�BCF���������AE��BE�ij���Ȼ�����ù��ɶ���������⣻
��2������AC������֤����ADC�ǵȱ������Σ���֤����AFD�ա�AEC��HL��������ȫ�������εĶ�Ӧ����ȼ���֤�ã�
��3������AM������֤����ABE�ա�ACD��Ȼ��֤��Rt��ABM��Rt��ACM��HL��������ȫ�������εĶ�Ӧ����ȣ��Լ�����ֱ�������� ������֤����MBC=��MED����ED��BC����֤�ã�
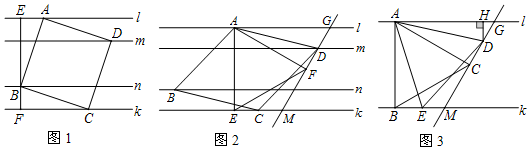
���  �⣺��1����ͼ1��
�⣺��1����ͼ1��
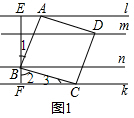
��BE��l��l��k��
���AEB=��BFC=90�㣬
���ı���ABCD�������Σ�
���1+��2=90�㣬AB=BC����2+��3=90�㣬
���1=��3��
���ڡ�ABE�͡�BCF�У�
$\left\{\begin{array}{l}{��1=��3}\\{��AEB=��BFC}\\{AB=BC}\end{array}\right.$��
���ABE�ա�BCF��AAS����
��AE=BF=1��
��BE=d1+d2=3��
��AB=$\sqrt{{3}^{2}+{1}^{2}}$=$\sqrt{10}$��
�������εı߳���$\sqrt{10}$��
��2����ͼ2 ������AC��
������AC��
���ı���ABCD�����Σ�
��AD=DC��
�֡�ADC=60�㣬
���ADC�ǵȱ������Σ�
��AD=AC��
��AE��k����AFD=90�㣬
���AEC=��AFD=90�㣬
�ߡ�AEF�ǵȱ������Σ�
��AF=AE��
��Rt��AFD��Rt��ACE��
$\left\{\begin{array}{l}{AF=AE}\\{AC=AD}\end{array}\right.$��
���AFD�ա�AEC��HL����
��EC=DF��
��3����ͼ4��
��2��DH��4ʱ��BC��DE��
�������£�����AM��
��AB��k����ACD=90�㣬
���ABE=��ACD=90�㣬
�ߡ�ABC�ǵȱ������Σ�
��AB=AC��
���ڡ�ABE�͡�ACD�У�
$\left\{\begin{array}{l}{AB=AC}\\{AE=AD}\end{array}\right.$��
���ABE�ա�ACD��HL����
��BE=CD��
����Rt��ABM��Rt��ACM��
$\left\{\begin{array}{l}{AB=AC}\\{AM=AN}\end{array}\right.$��
��Rt��ABM��Rt��ACM��HL����
��BM=CM��
���MBC=��MCB
��MB=MC��
���MED=��MDE��
���ڵ���������MDE�͵���������MCB�У���DME=��CMB��
���MBC=��MED��
��ED��BC��
���� ���������ı��ε��ۺ��⣮�����������ε����ʡ�ȫ�������ε��ж������ʡ����������ε��ж��������Լ����ɶ�����֪ʶ��ע��ȷ�����������ǽ����Ĺؼ���


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ����һ�麬��45���ֱ�������ε������������ֱ�ߵĶԱ��ϣ������1=20�㣬��ô��2�Ķ����ǣ�������
��ͼ����һ�麬��45���ֱ�������ε������������ֱ�ߵĶԱ��ϣ������1=20�㣬��ô��2�Ķ����ǣ�������| A�� | 15�� | B�� | 20�� | C�� | 30�� | D�� | 25�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 3 | B�� | 4 | C�� | 7 | D�� | 10 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
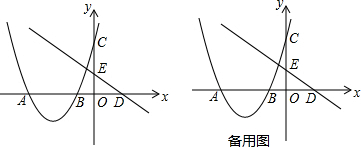
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -1 | B�� | 0 | C�� | 2 | D�� | -2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
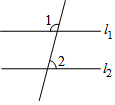 ��ͼ��l1��l2����1=110�㣬���2�Ķ����ǣ�������
��ͼ��l1��l2����1=110�㣬���2�Ķ����ǣ�������| A�� | 68�� | B�� | 70�� | C�� | 105�� | D�� | 110�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com