
分析 (1)根据解一元一次不等式的方法可以求得相应的解集,从而可以在数轴上表示出这个解集;
(2)根据解一元一次不等式的方法可以求得相应的解集,从而可以在数轴上表示出这个解集,本题得以解决.
解答 解:(1)3x+2≤8
移项及合并同类项,得
3x≤6
系数化为1,得
x≤2,
故原不等式的解集是x≤2,在数轴上表示如下所示,
(2)-$\frac{1}{4}$x+2<-8-2x
移项及合并同类项,得
$\frac{7}{4}x<-10$
系数化为1,得
$x<\frac{-40}{7}$
故原不等式的解集是x<$\frac{-40}{7}$,在数轴上表示如下所示,
点评 本题考查解一元一次不等式和在数轴上表示不等式的解集,解题的关键是明确解一元一次不等式的方法,可以在数轴上表示相应的解集.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
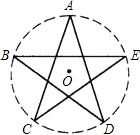 如图为我国国旗上的五角星(即点A、B、C、D、E为圆的五等分点),已知AC=a,则此五角星的外接圆直径可表示为( )
如图为我国国旗上的五角星(即点A、B、C、D、E为圆的五等分点),已知AC=a,则此五角星的外接圆直径可表示为( )| A. | a•sin72° | B. | $\frac{a}{tan72°}$ | C. | $\frac{a}{cos18°}$ | D. | $\frac{a}{cos36°}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图所示的象棋盘上网格是由小正方形组成,若帅位于点(-2,-2)上,相位于点(2,-2)上,则炮位于点( )
如图所示的象棋盘上网格是由小正方形组成,若帅位于点(-2,-2)上,相位于点(2,-2)上,则炮位于点( )| A. | (-5,1) | B. | (-3,1) | C. | (-8,2) | D. | (-3,3) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
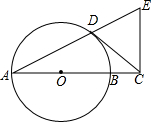 已知AB为⊙O的直径,点D为⊙O上一点,过点D作⊙O的切线,交AB的延长线于点C,过点C作AC的垂线,交AD的延长线于点E
已知AB为⊙O的直径,点D为⊙O上一点,过点D作⊙O的切线,交AB的延长线于点C,过点C作AC的垂线,交AD的延长线于点E查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com