
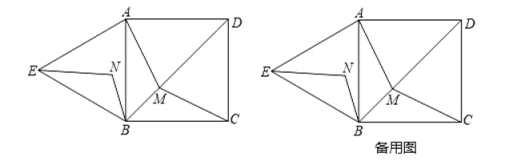
【题目】如图,四边形![]() 是正方形,
是正方形,![]() 是等边三角形,
是等边三角形,![]() 为对角线
为对角线![]() (不含
(不含![]() 点)上任意一点,将
点)上任意一点,将![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 得到
得到![]() ,连接
,连接![]() 、
、![]() 、
、![]() .设点
.设点![]() 的坐标为
的坐标为![]() .
.
(1)若建立平面直角坐标系,满足原点在线段![]() 上,点
上,点![]() ,
,![]() .且
.且![]() (
(![]() ),则点
),则点![]() 的坐标为 ,点
的坐标为 ,点![]() 的坐标为 ;请直接写出点
的坐标为 ;请直接写出点![]() 纵坐标
纵坐标![]() 的取值范围是 ;
的取值范围是 ;
(2)若正方形的边长为2,求![]() 的长,以及
的长,以及![]() 的最小值. (提示:连结
的最小值. (提示:连结![]() :
:![]() ,
,![]() )
)
【答案】(1)![]() ,
,![]() ,
,![]() ;(2)
;(2)![]() ,
,![]() .
.
【解析】
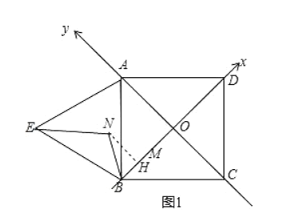
(1)如图1,以直线BD为x轴,直线AC为y轴,建立平面直角坐标系,根据正方形的性质得到OA=OB=OC=OD,由点B(-1,0),A(0,1),于是得到D(1,0),C(0,-1);过N作NH⊥BD于h,根据旋转的性质得到∠NBH=60°,BM=BN,求得NH=![]() BN=
BN=![]() t,于是得到结论;
t,于是得到结论;
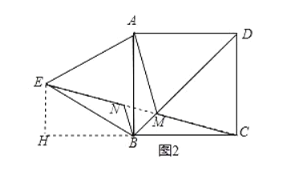
(2)如图所示,连接MN,过E作EH⊥BC,交CB的延长线于H,由旋转的性质得到BM=BN,∠NBM=60°,求得△BMN是等边三角形,求得MN=BM,根据等边三角形的性质得到BE=BA,∠ABE=60°,求得∠ABM=∠EBN,根据全等三角形的性质得到AM=EN,求得AM+BM+CM=EN+MN+CM,当E,N,M,C在同一直线上时,AM+BM+CN的最小值是CE的长,解直角三角形即可得到结论.
解:(1)如图1,以直线![]() 为
为![]() 轴,直线
轴,直线![]() 为
为![]() 轴,建立平面直角坐标系,
轴,建立平面直角坐标系,
∵四边形![]() 是正方形
是正方形
∴![]()
∵点![]() ,
,![]()
∴![]() ,
,![]()
过![]() 作
作![]() 于
于![]()
∴![]()
∵将![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 得到
得到![]() ,
,
∴![]()
∴![]()
∵![]()
∴点![]() 纵坐标
纵坐标![]() 的取值范围是
的取值范围是![]()
故答案为:![]() ,
,![]() ,
,![]()
(2)如图所示,连接![]() ,过
,过![]() 作
作![]() ,交
,交![]() 的延长线于
的延长线于![]() ,
,
由旋转可得,![]() ,
,![]() ,
,
∴![]() 是等边三角形,
是等边三角形,
∴![]()
∵![]() 是等边三角形
是等边三角形
∴![]()
∴![]()
∴![]() ≌
≌![]() (
(![]() )
)
∴![]()
∴![]()
∴当![]() ,
,![]() ,
,![]() ,
,![]() 在同一直线上时,
在同一直线上时,![]() 的最小值是
的最小值是![]() 的长,
的长,
又∵![]() ,
,![]()
∴![]()
∴![]() 中,
中,![]()
∴![]()
∴![]()
∴![]() 中,
中,![]()
∴![]() 的最小值为
的最小值为![]()


 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,一次函数y=﹣2x的图象与反比例函数y=![]() 的图象的一个交点为A(﹣1,n)
的图象的一个交点为A(﹣1,n)
(1)求反比例函数y=![]() 的表达式.
的表达式.
(2)若两函数图象的另一交点为B,直接写出B的坐标.
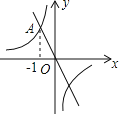
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小林有3张扑克牌,小丽有2张扑克牌,扑克牌上的数字如图所示。两人用这些扑克牌做游戏,他们分别从自己的扑克牌中随机抽取一张。
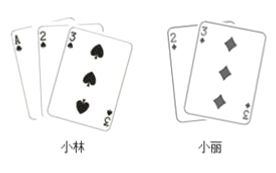
(1)求两人抽取的扑克牌上的数字之积为奇数的概率;(用“列表”或“画树状图”的方法说明);
(2)若两人抽取的扑克牌上的数字之积为奇数,则小林胜,否则小丽胜,这个游戏公平吗?若不公平,请修改游戏规则,使得游戏公平;若公平,请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点![]() 为坐标原点,抛物线
为坐标原点,抛物线![]() 与
与![]() 轴交于
轴交于![]() 、
、![]() 两点,顶点
两点,顶点![]() 在
在![]() 轴的正半轴上,且
轴的正半轴上,且![]() .
.
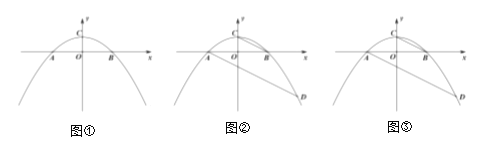
(1)如图①,求抛物线的解析式;
(2)如图②,连接![]() ,过点
,过点![]() 作
作![]() 的平行线,交第四象限的抛物线于点
的平行线,交第四象限的抛物线于点![]() ,求点
,求点![]() 的坐标;
的坐标;
(3)在(2)的条件下,点![]() 在第四象限的抛物线上,过点
在第四象限的抛物线上,过点![]() 作
作![]() 于点
于点![]() ,直线
,直线![]() 交
交![]() 轴于点
轴于点![]() ,过点
,过点![]() 作
作![]() 轴的垂线,垂足为
轴的垂线,垂足为![]() ,点
,点![]() 在
在![]() 的延长线上,连接
的延长线上,连接![]() 、
、![]() ,且
,且![]() ,若
,若![]() ,求点
,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
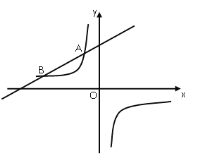
【题目】如图,一次函数![]() (
(![]() 为常数,且
为常数,且![]() )的图像与反比例函数
)的图像与反比例函数![]() 的图像交于
的图像交于![]() ,
,![]() 两点.
两点.
(1)求一次函数的表达式;
(2)若将直线![]() 向下平移
向下平移![]() 个单位长度后与反比例函数的图像有且只有一个公共点,求
个单位长度后与反比例函数的图像有且只有一个公共点,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线M:y=ax2+bx+c(a≠0)经过A(﹣1,0),且顶点坐标为B(0,1).
(1)求抛物线M的函数表达式;
(2)设F(t,0)为x轴正半轴上一点,将抛物线M绕点F旋转180°得到抛物线M1.
①抛物线M1的顶点B1的坐标为 ;
②当抛物线M1与线段AB有公共点时,结合函数的图象,求t的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】新春佳节,电子鞭炮因其安全、无污染开始走俏.某商店经销一种电子鞭炮,已知这种电子鞭炮的成本价为每盒80元,市场调查发现,该种电子鞭炮每天的销售量y(盒)与销售单价x(元)有如下关系:y=﹣2x+320(80≤x≤160).设这种电子鞭炮每天的销售利润为w元.
(1)求w与x之间的函数关系式;
(2)该种电子鞭炮销售单价定为多少元时,每天的销售利润最大?最大利润是多少元?
(3)该商店销售这种电子鞭炮要想每天获得2400元的销售利润,又想买得快.那么销售单价应定为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数的图象与x轴交于A(﹣3,0)和B(1,0)两点,交y轴于点C(0,3),点C、D是二次函数图象上的一对对称点,一次函数的图象过点B、D.
(1)请直接写出D点的坐标.
(2)求二次函数的解析式.
(3)根据图象直接写出使一次函数值大于二次函数值的x的取值范围.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com