
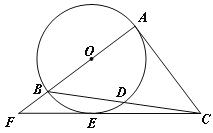
ЁОЬтФПЁПЁАжиЧьздШЛВЉЮяЙнЁБзјТфдкУРРіЕФчЦдЦЩННХЯТЃЌИУЙнЯжгаВиЦЗ11ЭђгрМўЃЌЪЧШЋЙњжааЁбЇЩњбабЇЪЕМљНЬг§ЛљЕиЃЌЮїДѓИНжаФГЪ§бЇаЫШЄаЁзщЃЌЯыВтСПВЉЮяЙнЕФИпЖШЃЌЫћУЧЯШдкВЉЮяЙне§ЖдУцЕФДѓТЅТЅЖЅAДІЃЌВтЕУВЉЮяЙнЕзВПBДІЕФИЉНЧЮЊ50ЁуЃЌВтЕУВЉЮяЙнЖЅЖЫCЕФИЉНЧЮЊ45ЁуЃЌдйДгТЅЕзOОЙ§ЦНЕиЕНДяFЃЌдйбизХаБЦТЯђЩЯЕНДяEЃЌзюКѓОЙ§ЦНЬЈДяЕНBЃЌВтЕУOFЃН20УзЃЌЦНЬЈEBЕФГЄЮЊ28.8УзЃЌвбжЊЃЌТЅOAИпЮЊ60.5УзЃЌаБЦТEFЕФЦТЖШiЃН1ЃК2.4ЃЌAЁЂOЁЂFЁЂEЁЂBЁЂCдкЭЌвЛЦНУцФкЃЌдђВЉЮяЙнЕФИпдМЮЊ(ЁЁЁЁ)УзЃЎ(ВЮПМЪ§ОнЃКtan50ЁуЁж1.2)
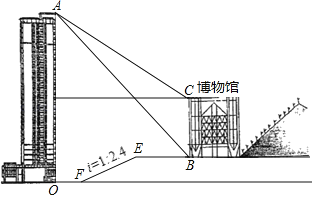
A.10.5B.10.0C.12.0D.12.2
ЁОД№АИЁПB
ЁОНтЮіЁП
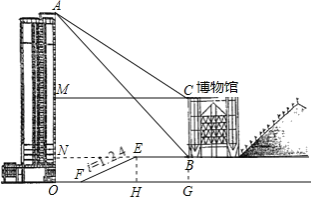
бгГЄCBНЛOFЕФбгГЄЯпгкGЃЌзїEHЁЭOGгкHЃЌбгГЄEBНЛOAгкNЃЌзїCMЁЭOAгкMЃЌЩшВЉЮяЙнЕФИпBCЮЊxУзЃЌAMЃНyУзЃЌИљОнЦТЖШЕФИХФюгУxЁЂyБэЪОГіFHЁЂEHЃЌИљОне§ЧаЕФЖЈвхСаГіЗНГЬЃЌНтЗНГЬЕУЕНД№АИЃЎ
НтЃКбгГЄCBНЛOFЕФбгГЄЯпгкGЃЌзїEHЁЭOGгкHЃЌбгГЄEBНЛOAгкNЃЌзїCMЁЭOAгкMЃЌ
дђЫФБпаЮMNBCЮЊОиаЮЃЌ
ЁрMCЃНOGЃЌMNЃНBCЃЌ
ЩшВЉЮяЙнЕФИпBCЮЊxУзЃЌAMЃНyУзЃЌ
дђMNЃНxЃЌ
ЁпЁЯACMЃН45ЁуЃЌ
ЁрMCЃНAMЃНyЃЌ
ЁрONЃН60.5ЉxЉyЃЌ
дђEHЃНONЃН60.5ЉxЉyЃЌ
ЁпаБЦТEFЕФЦТЖШiЃН1ЃК2.4ЃЌ
ЁрFHЃН2.4ЁСЃЈ60.5ЉxЉyЃЉЃЌ
ЁрOGЃНOF+FH+HGЃН20+2.4ЁСЃЈ60.5ЉxЉyЃЉ+28.8ЃНyЃЌ
ећРэЕУЃЌ2.4x+3.4yЃН194ЃЌ
дкRtЁїABNжаЃЌtanЁЯABNЃН![]() ЃЌМД
ЃЌМД![]()
ећРэЕУЃЌyЃН5xЃЌ
АбyЃН5xДњШы2.4x+3.4yЃН194ЃЌЕУxЃН10ЃЌМДBCЃН10УзЃЌ
ЙЪбЁЃКBЃЎ


 ЬьЬьЯђЩЯвЛБОКУОэЯЕСаД№АИ
ЬьЬьЯђЩЯвЛБОКУОэЯЕСаД№АИ аЁбЇЩњ10ЗжжггІгУЬтЯЕСаД№АИ
аЁбЇЩњ10ЗжжггІгУЬтЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдк ABCDжаЃЌCD=2ADЃЌBEЁЭADгкЕуEЃЌFЮЊDCЕФжаЕуЃЌСЌНсEFЁЂBFЃЌЯТСаНсТлЃКЂйЁЯABC=2ЁЯABFЃЛЂкEF=BFЃЛЂлSЫФБпаЮDEBC=2SЁїEFBЃЛЂмЁЯCFE=3ЁЯDEF,Цфжае§ШЗНсТлЕФИіЪ§ЙВгаЃЈ ЃЉ.

A. 1Иі B. 2Иі C. 3Иі D. 4Иі
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЮЊСЫгНгЁАЮхвЛЁБаЁГЄМйЕФЙКЮяИпЗхЃЎФГЗўзАзЈТєЕъРЯАхаЁЭѕзМБИЙКНјМзЁЂввСНжжЯФМОЗўзАЃЎЦфжаМзжжЗўзАУПМўЕФГЩБОМлБШввжжЗўзАЕФГЩБОМлЖр20дЊЃЌМзжжЗўзАУПМўЕФЪлМлЮЊ240дЊБШввжжЗўзАЕФЪлМлЖр80дЊЃЎаЁЭѕгУ4000дЊЙКНјМзжжЗўзАЕФЪ§СПгыгУ3200дЊЙКНјввжжЗўзАЕФЪ§СПЯрЭЌЃЎ
ЃЈ1ЃЉМзжжЗўзАУПМўЕФГЩБОЪЧЖрЩйдЊЃП
ЃЈ2ЃЉвЊЪЙЙКНјЕФМзЁЂввСНжжЗўзАЙВ200МўЕФзмРћШѓЃЈРћШѓ=ЪлМл-НјМлЃЉВЛЩйгк21100дЊЃЌЧвВЛГЌЙ§21700дЊЃЌЮЪаЁЭѕгаМИжжНјЛѕЗНАИЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЃКЪЕЪ§xТњзу2aЉ3ЁмxЁм2a+2ЃЌy1ЃНx+aЃЌy2ЃНЉ2x+a+3ЃЌЖдгкУПвЛИіxЃЌpЖМШЁy1ЃЌy2жаЕФНЯДѓжЕЃЎШєpЕФзюаЁжЕЪЧa2Љ1ЃЌдђaЕФжЕЪЧЃЈЁЁЁЁЃЉ
A.0ЛђЉ3B.2ЛђЉ1C.1Лђ2D.2ЛђЉ3
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЖўДЮКЏЪ§y1ЃНx2+bx+cгыy2ЃНx2+cx+bЃЈbЃМcЃЉЕФЭМЯѓЯрНЛгкЕуAЃЌЗжБ№гыyжсЯрНЛгкЕуCЃЌBЃЌСЌНгABЁЂACЃЎ
ЃЈ1ЃЉЙ§ЕуЃЈ1ЃЌ0ЃЉзїжБЯпlЦНаагкyжсЃЌХаЖЯЕуAгыжБЯпlЕФЮЛжУЙиЯЕЃЌВЂЫЕУїРэгЩЃЎ
ЃЈ2ЃЉЕБAЁЂCСНЕуЪЧЖўДЮКЏЪ§y1ЃНx2+bx+cЭМЯѓЩЯЕФЖдГЦЕуЪБЃЌЧѓbЕФжЕЃЎ
ЃЈ3ЃЉЕБЁїABCЪЧЕШБпШ§НЧаЮЪБЃЌЧѓЕуBЕФзјБъЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГПЮЭтбЇЯАаЁзщИљОнбЇЯАКЏЪ§ЕФОбщЃЌЖдКЏЪ§yЃНx3Љ3xЕФЭМЯѓгыаджЪНјааСЫЬНОПЃЎЧыВЙГфЭъећвдЯТЬНЫїЙ§ГЬЃК
(1)СаБэЃК
x | Ё | Љ2 |
| Љ1 |
| 0 |
| 1 |
| 2 | Ё |
y | Ё | Љ2 | m | 2 |
| 0 |
| n |
| 2 | Ё |
ЧыжБНгаДГіmЃЌnЕФжЕЃЛ
(2)ИљОнЩЯБэжаЕФЪ§ОнЃЌдкЦНУцжБНЧзјБъЯЕФкВЙШЋИУКЏЪ§ЕФЭМЯѓЃЛ
(3)ШєКЏЪ§yЃНx3Љ3xЕФЭМЯѓЩЯгаШ§ИіЕуA(x1ЃЌy1)ЃЌB(x2ЃЌy2)ЃЌC(x3ЃЌy3)ЃЌЧвx1ЃМЉ2ЃМx2ЃМ2ЃМx3ЃЌдђy1ЃЌy2ЃЌy3жЎМфЕФДѓаЁЙиЯЕЮЊЁЁ ЁЁ(гУЁАЃМЁБСЌНг)ЃЛ
(4)ШєЗНГЬx3Љ3xЃНkгаШ§ИіВЛЭЌЕФЪЕЪ§ИљЃЎЧыИљОнКЏЪ§ЭМЯѓЃЌжБНгаДГіkЕФШЁжЕЗЖЮЇЃЎ
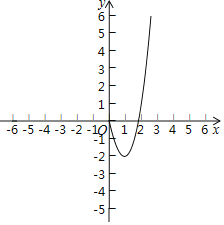
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌ![]() ЪЧ
ЪЧ![]() ЕФжБОЖЃЌЕу
ЕФжБОЖЃЌЕу![]() дк
дк![]() ЩЯЃЌ
ЩЯЃЌ![]() ЕФЦНЗжЯпНЛ
ЕФЦНЗжЯпНЛ![]() гкЕу
гкЕу![]() ЃЌНЛ
ЃЌНЛ![]() гкЕу
гкЕу![]() ЃЎЙ§Еу
ЃЎЙ§Еу![]() зї
зї![]() ЕФЧаЯп
ЕФЧаЯп![]() НЛ
НЛ![]() ЕФбгГЄЯпгкЕу
ЕФбгГЄЯпгкЕу![]() ЃЌСЌНг
ЃЌСЌНг![]() ЃЌ
ЃЌ![]() ЃЎ
ЃЎ
ЃЈ1ЃЉЧѓжЄЃК![]() ЃЌ
ЃЌ![]() ЃЛ
ЃЛ
ЃЈ2ЃЉЙ§Еу![]() ЗжБ№зїжБЯп
ЗжБ№зїжБЯп![]() ЃЌ
ЃЌ![]() ДЙЯпЃЌДЙзуЮЊ
ДЙЯпЃЌДЙзуЮЊ![]() ЃЌ
ЃЌ![]() ЃЎШє
ЃЎШє![]() ЃЌ
ЃЌ![]() ЃЌЧыФуЭъГЩЪОвтЭМВЂЧѓЯпЖЮ
ЃЌЧыФуЭъГЩЪОвтЭМВЂЧѓЯпЖЮ![]() ЕФГЄЃЎ
ЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМ1ЃЌХзЮяЯпy=Љx2+bx+cОЙ§AЃЈЉ1ЃЌ0ЃЉЃЌBЃЈ4ЃЌ0ЃЉСНЕуЃЌгыyжсЯрНЛгкЕуCЃЌСЌНсBCЃЌЕуPЮЊХзЮяЯпЩЯвЛЖЏЕуЃЌЙ§ЕуPзїxжсЕФДЙЯпlЃЌНЛжБЯпBCгкЕуGЃЌНЛxжсгкЕуEЃЎ
ЃЈ1ЃЉЧѓХзЮяЯпЕФБэДяЪНЃЛ
ЃЈ2ЃЉЕБPЮЛгкyжсгвБпЕФХзЮяЯпЩЯдЫЖЏЪБЃЌЙ§ЕуCзїCFЁЭжБЯпlЃЌFЮЊДЙзуЃЌЕБЕуPдЫЖЏЕНКЮДІЪБЃЌвдPЃЌCЃЌFЮЊЖЅЕуЕФШ§НЧаЮгыЁїOBCЯрЫЦЃПВЂЧѓГіДЫЪБЕуPЕФзјБъЃЛ

ЃЈ3ЃЉШчЭМ2ЃЌЕБЕуPдкЮЛгкжБЯпBCЩЯЗНЕФХзЮяЯпЩЯдЫЖЏЪБЃЌСЌНсPCЃЌPBЃЌЧыЮЪЁїPBCЕФУцЛ§SФмЗёШЁЕУзюДѓжЕЃПШєФмЃЌЧыЧѓГізюДѓУцЛ§SЃЌВЂЧѓГіДЫЪБЕуPЕФзјБъЃЌШєВЛФмЃЌЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
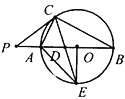
ЁОЬтФПЁПШчЭМЃЌRtЁїABCжаЃЌЁЯA=90ЁуЃЌвдABЮЊжБОЖЕФЁбOНЛBCгкЕуDЃЌЕуEдкЁбOЩЯЃЌ CE=CAЃЌ
ABЃЌCEЕФбгГЄЯпНЛгкЕуFЃЎ
ЃЈ1ЃЉЧѓжЄЃКCEгыЁбOЯрЧаЃЛ
ЃЈ2ЃЉШєЁбOЕФАыОЖЮЊ3ЃЌEF=4ЃЌЧѓBDЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com