
【题目】如图所示,点D在![]() 的AB边上,且
的AB边上,且![]() .
.
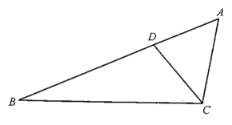
(1)作![]() 的平分线DE,交BC于点E(用尺规作图法,保留作图痕迹,不要求写作法);
的平分线DE,交BC于点E(用尺规作图法,保留作图痕迹,不要求写作法);
(2)在(1)的条件下,判断直线DE与直线AC的位置关系.
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】某学校准备为七年级学生开设![]() 共6门选修课,选取了若干学生进行了我最喜欢的一门选修课调查,将调查结果绘制成了如图所示的统计图表(不完整).
共6门选修课,选取了若干学生进行了我最喜欢的一门选修课调查,将调查结果绘制成了如图所示的统计图表(不完整).
选修课 |
|
|
|
|
|
|
人数 | 40 | 60 | 100 |
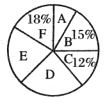
下列说法不正确的是( )
A.这次被调查的学生人数为400人B.![]() 对应扇形的圆心角为
对应扇形的圆心角为![]()
C.喜欢选修课![]() 的人数为72人D.喜欢选修课
的人数为72人D.喜欢选修课![]() 的人数最少
的人数最少
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图∠1=∠2,CF⊥AB,DE⊥AB,求证:FG∥BC.
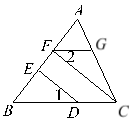
证明:∵CF⊥AB,DE⊥AB (已知)
∴∠BED=90°,∠BFC=90°( )
∴∠BED=∠BFC ( )
∴ED∥FC ( )
∴∠1=∠BCF ( )
∵∠2=∠1 ( 已知 )
∴∠2=∠BCF ( )
∴FG∥BC ( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),E是直线AB、CD内部一点,AB∥CD,连接EA、ED.
(1)探究:
①若∠A=30°,∠D=40°,则∠AED等于多少度?
②若∠A=20°,∠D=60°,则∠AED等于多少度?
③在图(1)中∠AED、∠EAB、∠EDC有什么数量关系,并证明你的结论.
(2)拓展:如图(2),射线FE与矩形ABCD的边AB交于点E,与边CD交于点F,①②③④分别是被射线FE隔开的四个区域(不含边界,其中③④位于直线AB的上方),P是位于以上四个区域上点,猜想:∠PEB、∠PFC、∠EPF之间的关系.(不要求证明)

查看答案和解析>>
科目:初中数学 来源: 题型:
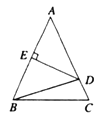
【题目】如图,在△ABC中,AB=AC,AB的垂直平分线分别交AC、AB于点D、E,若△ABC和△BDC 的周长分别为40cm和25cm ,则BC=_______
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】蜗牛从某点![]() 开始沿东西方向的直线爬行,规定向东爬行的路程记为正数,向西爬行的路程记为负数.爬过的各段路程依次为(单位:厘米):
开始沿东西方向的直线爬行,规定向东爬行的路程记为正数,向西爬行的路程记为负数.爬过的各段路程依次为(单位:厘米):![]()
(1)蜗牛最后是否回到出发点?请说明理由;
(2)蜗牛离开出发点![]() 最远时是_______厘米;
最远时是_______厘米;
(3)在爬行过程中,如果蜗牛每爬2厘米奖励一粒芝麻,求蜗牛-共得到多少粒芝麻?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com