
����Ŀ��ij������������ÿ̨����Ϊ120Ԫ��170Ԫ��A��B�����ͺŵĵ���ȣ������ʾ�ǽ�2�ܵ���������������ۡ��ۼ۾����ֲ��䣬����=��������һ�����ɱ���
����ʱ�� | �������� | �������� | |
A���ͺ� | B���ͺ� | ||
��һ�� | 6 | 5 | 2200Ԫ |
�ڶ��� | 4 | 10 | 3200Ԫ |
��1����A��B�����ͺŵĵ���ȵ����۵��ۣ�
��2���������ٲɹ��������ͺŵĵ���ȹ�130̨������ȫ�������꣬�ó����ܷ�ʵ����������������Ϊ8010Ԫ��Ŀ�ꣿ���ܣ��������Ӧ�IJɹ������������ܣ���˵�����ɣ�
���𰸡���1��A���ͺŵĵ���ȵ����۵���Ϊ150Ԫ/̨��B���ͺŵĵ���ȵ����۵���Ϊ260Ԫ/̨����2�������ٲɹ�A���ͺŵ����89̨��B���ͺŵ����41̨��
��������
��1����A���ͺŵĵ���ȵ����۵���ΪxԪ/̨��B���ͺŵĵ���ȵ����۵���ΪyԪ/̨�������ܼ�=���ۡ��������ǰ���ܵ����ۼ�¼�����ɵó�����x��y�Ķ�Ԫһ�η����飬��֮���ɵó����ۣ���2���蹺��A���ͺŵ����m̨����B���ͺŵ���ȣ�130��m��̨����������=��������һ�����ɱ������ɵó�����m��һԪһ�η��̣���֮���ɵó����ۣ�
��1����A���ͺŵĵ���ȵ����۵���ΪxԪ/̨��B���ͺŵĵ���ȵ����۵���ΪyԪ/̨��
��������ã�![]() ��
��
��ã�![]() ��
��
��A���ͺŵĵ���ȵ����۵���Ϊ150Ԫ/̨��B���ͺŵĵ���ȵ����۵���Ϊ260Ԫ/̨��
��2���蹺��A���ͺŵ����m̨����B���ͺŵ���ȣ�130��m��̨��
��������ã�2200+3200+150m+260��130��m����120����6+4+m����170[5+10+��130��m��]=8010��
��ã�m=89��
��130��m=41��
�𣺳����ٲɹ�A���ͺŵ����89̨��B���ͺŵ����41̨��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ֱ��AB��һ��OΪ�˵�������OC����һ��ֱ�����ǰ��ֱ�Ƕ������O��(ע����DOE��90��).
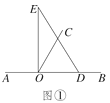

(1)��ͼ�٣���ֱ�����ǰ�DOE��һ��OD��������OB��������BOC��60�㣬����COE�Ķ�����
(2)��ͼ�ڣ�������DOE��O��ʱ��ת����ij��λ��ʱ����ǡ������5��COD����AOE������BOC��60�㣬����BOD�Ķ�����
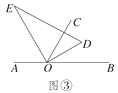
(3)��ͼ�ۣ���ֱ�����ǰ�DOE�Ƶ�O��ʱ�뷽��ת����ij��λ������OEǡ��ƽ����AOC����˵��OD������������BOC��ƽ����.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���κ���y=ax2��bx+2��a��0��ͼ��Ķ����ڵڶ����ޣ��ҹ��㣨1��0������a��ȡֵ��Χ������a+b��ֵΪ������������b��ֵΪ ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD�У�AB=8����һ��ƽ�Ƴ�����ABCD��AB�ķ�������ƽ��6����λ���õ�������A1B1C1D1����2��ƽ�ƽ�������A1B1C1D1��A1B1�ķ�������ƽ��6����λ���õ�������A2B2C2D2��������n��ƽ�ƽ�������An��1Bn��1 Cn��1 Dn��1 �ķ���ƽ��6����λ���õ�������AnBnCnDn��n��2������ABn�ij���Ϊ2018����n��ֵΪ��������

A. 334 B. 335 C. 336 D. 337
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ԭ�⣩��ֱ֪��AB��CD����PΪƽ����AB��CD֮���һ�㣮��ͼ1������ABP=50�㣬��CDP=60�㣬BEƽ����ABP��DEƽ����CDP������BED�Ķ�����
��̽������ͼ2������P��ֱ��AB���Ϸ�ʱ������ABP=������CDP=�£���ABP����CDP��ƽ���߽��ڵ�E1����ABE1����CDE1�Ľ�ƽ���߽��ڵ�E2����ABE2����CDE2�Ľ�ƽ���߽��ڵ�E3�����Դ����ƣ�����En�Ķ�����
����ʽ����ͼ3����ABP�Ľ�ƽ���ߵķ����ӳ��ߺ���CDP�IJ��ǵĽ�ƽ���߽��ڵ�E���Բ�����P����E��������ϵ����˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��l1�Ľ���ʽΪy=��x+2��l1��x�ύ�ڵ�B��ֱ��l2������D��0��5������ֱ��l1���ڵ�C����1��m��������x�ύ�ڵ�A,
��1�����C�����꼰ֱ��l2�Ľ���ʽ��
��2������ABC�������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������һ����Ϊ1��ľ�ˣ���1�ν�ȡ�䳤�ȵ�һ�룬��2�ν�ȡ���1��ʣ�³��ȵ�һ�룬��3�ν�ȡ���2��ʣ�³��ȵ�һ�룬��˷�����ȡ�����n��nΪ���������ν�ȡ��ľ��ʣ�µij���Ϊ�ף�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���۲����е�ʽ��
��1����ʽ��a1=![]() =
=![]() ��
��![]() ��
��
��2����ʽ��a2=![]() =
=![]() ��
��![]() ��
��
��3����ʽ��a3=![]() =
=![]() ��
��![]() ��
��
��4����ʽ��a4=![]() =
=![]() ��
��![]() ��
��
���������ɣ��ش��������⣺
��1���ú�n�Ĵ���ʽ��ʾ��n����ʽ��an=_____=_____��
��2��ʽ��a1+a2+a3+��+a20=_____��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com