由方程x2+4x+4=0的根为x1=x2=-2,可得x1+x2=-4,x1.x2=4,则
(1)方程x2-5x+6=0的根为x1=______,x2=______,x1+x2=______,x1.x2=______;
(2)x1,x2是方程ax2+bx+c=0的两个根,则x1+x2=______,x1.x2=______;
(3)已知x1,x2(其中x1>x2)是方程2x2+5x-2=0的两个根,由(2)的结论,不解方程求①x12+x22,②x1-x2的值.
【答案】
分析:(1)把方程x
2-5x+6=0进行因式分解,求出x
1、x
2的值即可;
(2)根据方程根与系数的关系直接解答即可;
(3)由方程根与系数的关系分别求出x
1+x
2,x
1.x
2的值,代入x
12+x
22及x
1-x
2进行计算.
解答:解:(1)∵方程x
2-5x+6=0可化为(x-2)(x-3)=0,
∴x
1=2,x
2=3,
∴x
1+x
2=5,x
1.x
2=6,
故答案为:2,3,5,6.(2分)
(2)∵x
1,x
2是方程ax
2+bx+c=0的两个根,
∴x
1+x
2=-
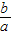
,x
1.x
2=
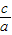
;
故答案为:

,

;(4分)
(3)∵

,
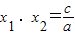
,
∴
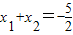
,x
1.x
2=-1,
∴x
12+x
22=

,(7分)

(10分)
点评:本题考查的是一元二次方程根与系数的关系及用因式分解法解一元二次方程,熟知一元二次方程根与系数的关系是解答此题的关键,即x
1,x
2是一元二次方程ax
2+bx+c=0(a≠0)的两根时,x
1+x
2=-
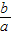
,x
1x
2=

.

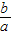 ,x1.x2=
,x1.x2=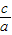 ;
; ,
, ;(4分)
;(4分) ,
,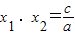 ,
,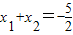 ,x1.x2=-1,
,x1.x2=-1, ,(7分)
,(7分) (10分)
(10分)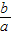 ,x1x2=
,x1x2= .
. 

 智能训练练测考系列答案
智能训练练测考系列答案