
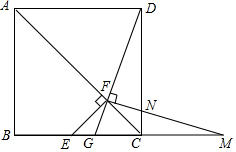
 如图.在正方形ABCD中,点E是BC边上的中点,EF⊥AC于点F.连接DF并延长交BC于G.过F作FM⊥DG交CD于N,交BC的延长线于点M.
如图.在正方形ABCD中,点E是BC边上的中点,EF⊥AC于点F.连接DF并延长交BC于G.过F作FM⊥DG交CD于N,交BC的延长线于点M.分析 (1)先由正方形的性质得出,∠FEC=∠ECF=45°,进而得出EF=CF,即可得出结论;
(2)先判断出△GHF∽△GCD得出$\frac{GH}{CG}=\frac{FH}{CD}$,再用等腰直角三角形的性质得出EC=2a,CD=4a,即可得出GH,即可得出结论;
(3)先判断出△MFG≌△DFN,即可得出CM=CE,借助(2)的结论求出CM=3,FH=$\frac{3}{2}$,最后用三角形的面积公式即可得出结论.
解答 (1)证:∵AC是正方形的对角线,
∴∠ACD=∠ACB=45°,
∵EF⊥AC,
∴∠EFC=90°,
∴∠FEC=∠ECF=45°,
∴EF=CF,
∵∠CFE=∠GFN=90°,
∴∠EFG=∠CFN,
在△FEG和△FCN中,$\left\{\begin{array}{l}{∠FEG=∠FCN}\\{EF=CF}\\{∠EFG=∠CFN}\end{array}\right.$,
∴△FEG≌△FCN;
(2)解:CG=2EG,
理由:
如图,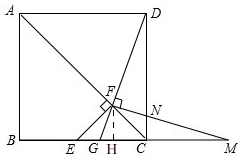 过点F作FH⊥BC于H,
过点F作FH⊥BC于H,
∴FH∥DC,
∴△GHF∽△GCD,
∴$\frac{GH}{CG}=\frac{FH}{CD}$,
设FH=a,
∴EH=CH=FN=a,
∴EC=2a,
∵E是正方形ABCD的边BC中点,
∴CD=BC=2CE=4a,
∵CG=GH+CH=a+GH,
∴$\frac{GH}{a+GH}$=$\frac{1}{4}$,
∴GH=$\frac{1}{3}$a,
∴EG=EH-GH=a-$\frac{1}{3}$a=$\frac{2}{3}$a,CG=CH+GH=a+$\frac{1}{3}$a=$\frac{4}{3}$a,
∴CG=2EG;
(3)由(1)知,△FEG≌△FCN,
∴FG=FN,
在△MFG和△DFN中,$\left\{\begin{array}{l}{∠M=∠FDN}\\{∠MFG=∠DFN}\\{FG=FN}\end{array}\right.$,
∴△MFG≌△DFN,
∴MG=DN,
∴ME=CD=BC,
∵点E是BC的中点,
∴CM=CE,
设FH=a,
由(2)知,BC=4a,CE=2a,
∴CM=2a,
∵AB=6,
∴4a=6,
∴a=$\frac{3}{2}$,
∴FH=a=$\frac{3}{2}$,CM=2a=3,
∴S△FCM=$\frac{1}{2}$CM•FH=$\frac{1}{2}$×3×$\frac{3}{2}$=$\frac{9}{4}$.
点评 此题是四边形综合题,主要考查了正方形的性质,等腰直角三角形的性质,全等三角形的判定和性质,相似三角形的判定和性质,三角形的面积公式,解(1)的关键是得出EF=CF,解(2)的关键是得出GH,解(3)的关键是判断出△MFG≌△DFN,是一道很好的中考常考题.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
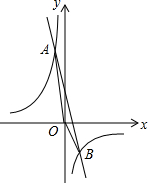 如图,已知反比例函数y=$\frac{{k}_{1}}{x}$与一次函数y=k2x+b的图象交于A(-1,10),B(2,n)两点.
如图,已知反比例函数y=$\frac{{k}_{1}}{x}$与一次函数y=k2x+b的图象交于A(-1,10),B(2,n)两点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
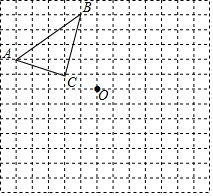 按下列要求在方格纸中画图:
按下列要求在方格纸中画图:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com