
ЁОЬтФПЁПШчЭМЃЌдквЛеХЦНааЫФБпаЮжНЦЌABCDжаЃЌЛвЛИіСтаЮЃЌМзЁЂввСНЮЛЭЌбЇЕФЛЗЈШчЯТЃКМзЃКвдBЃЌAЮЊдВаФЃЌABГЄЮЊАыОЖзїЛЁЃЌЗжБ№НЛBCЃЌADгкЕуEЃЌFЃЌдђЫФБпаЮABEFЮЊСтаЮЃЛввЃКзїЁЯAЃЌЁЯBЕФЦНЗжЯпAEЃЌBFЃЌЗжБ№НЛBCгкЕуEЃЌНЛADгкЕуFЃЌдђЫФБпаЮABEFЪЧСтаЮЃЛЙигкМзЁЂввСНШЫЕФЛЗЈЃЌЯТСаХаЖЯе§ШЗЕФЪЧЃЈЁЁЁЁЃЉ
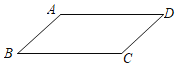
A. НіМзе§ШЗB. Нівве§ШЗ
C. МзЁЂввОље§ШЗD. МзЁЂввОљДэЮѓ
ЁОД№АИЁПC
ЁОНтЮіЁП
ИљОнЛљБОзїЭМвдМАСтаЮЕФХаЖЈПЩжЊМзввЖМЪЧе§ШЗЕФЃЎ
НтЃКМзЕФзїЗЈе§ШЗЃКЁпAF=ABЃЌBE=AB
ЁрAF=BEЃЌ
дкABCDжаЃЌADЁЮBCЃЎ
МДAFЁЮBEЃЎ
ЁрЫФБпаЮABEFЮЊЦНааЫФБпаЮЃЎ
ЁпAF=ABЃЌ
ЁрЫФБпаЮABEFЮЊСтаЮЃЈСкБпЯрЕШЕФЦНааЫФБпаЮЪЧСтаЮЃЉЃЎ
ввЕФзїЗЈе§ШЗЃЛ
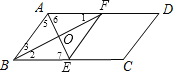
ЁпADЁЮBCЃЌ
ЁрЁЯ1=ЁЯ2ЃЌЁЯ6=ЁЯ7ЃЌ
ЁпBFЦНЗжЁЯABCЃЌAEЦНЗжЁЯBADЃЌ
ЁрЁЯ2=ЁЯ3ЃЌЁЯ5=ЁЯ6ЃЌ
ЁрЁЯ1=ЁЯ3ЃЌЁЯ5=ЁЯ7ЃЌ
ЁрAB=AFЃЌAB=BEЃЌ
ЁрAF=BE
ЁпAFЁЮBEЃЌЧвAF=BEЃЌ
ЁрЫФБпаЮABEFЪЧЦНааЫФБпаЮЃЌ
ЁпAB=AFЃЌ
ЁрЦНааЫФБпаЮABEFЪЧСтаЮЃЎ
ЙЪбЁЃКCЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
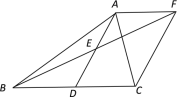
ЁОЬтФПЁПШчЭМЃЌдкЁїABCжаЃЌDЪЧBCБпЩЯЕФвЛЕуЃЌEЪЧADЕФжаЕуЃЌЙ§ЕуAзїBCЕФЦНааЯпНЛBEЕФбгГЄЯпгкFЃЌЧвAF=DCЃЌСЌНгCFЃЎ
ЃЈ1ЃЉЧѓжЄЃКDЪЧBCЕФжаЕуЃЛ
ЃЈ2ЃЉШчЙћAB=ACЃЌЪдХаЖЯЫФБпаЮADCFЕФаЮзДЃЌВЂжЄУїФуЕФНсТлЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊжБЯпlЩЯгавЛЕуOЃЌЕуAЃЌBЭЌЪБДгOГіЗЂЃЌдкжБЯпlЩЯЗжБ№ЯђзѓЃЌЯђгвзїдШЫйдЫЖЏЃЌЧвAЃЌBЕФЫйЖШжЎБШЪЧ1ЃК2ЃЌЩшдЫЖЏЪБМфЮЊtsЃЌ
ЃЈ1ЃЉЕБt=2sЪБЃЌAB=24cmЃЌДЫЪБЃЌ
ЂйдкжБЯпlЩЯЛГіAЃЌBСНЕудЫЖЏ2sЪБЕФЮЛжУЃЌВЂЛиД№ЕуAдЫЖЏЕФЫйЖШЪЧЁЁ ЁЁcm/sЃЌЕуBЕФдЫЖЏЫйЖШЪЧЁЁ ЁЁcm/sЃЛ
ЂкШєЕуPЮЊжБЯпlЩЯвЛЕуЃЌЧвPA=OP+PBЃЌЧѓ![]() ЕФжЕЃЛ
ЕФжЕЃЛ
ЃЈ2ЃЉдкЃЈ1ЃЉЕФЬѕМўЯТЃЌШєAЃЌBЭЌЪБАДдЫйЖШЯђзѓдЫЖЏЃЌдйОЙ§МИУыЃЌOA=3OBЃП

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
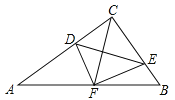
ЁОЬтФПЁПШчЭМЃЌдкЁїABCжаЃЌЁЯACB=90ЁуЃЌЕуDЃЌEЗжБ№дкACЃЌBCЩЯЃЌЧвЁЯCDE=ЁЯBЃЌНЋЁїCDEбиDEелЕўЃЌЕуCЧЁКУТфдкABБпЩЯЕФЕуFДІЃЎШєAC=8ЃЌAB=10ЃЌдђCDЕФГЄЮЊ ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
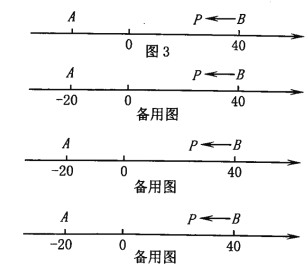
ЁОЬтФПЁПЃЈдФЖСРэНтЃЉЃКAЃЌBЃЌCЮЊЪ§жсЩЯШ§ЕуЃЌШєЕуCЕНAЕФОрРыCAЪЧЕуCЕНBЕФОрРыCBЕФ2БЖЃЌЮвУЧОЭГЦЕуCЪЧЃЈAЃЌBЃЉЕФКУЕу.Р§ШчЃЌШчЭМ1ЃЌЕуAБэЪОЕФЪ§ЮЊЃ1ЃЌЕуBБэЪОЕФЪ§ЮЊ2.БэЪО1ЕФЕуCЕНЕуAЕФОрРыCAЪЧ2ЃЌЕНЕуBЕФОрРыCBЪЧ1ЃЌФЧУДЕуCЪЧЃЈAЃЌBЃЉЕФКУЕуЃЛгжШчЃЌБэЪО0ЕФЕуDЕНЕуAЕФОрРыDAЪЧ1ЃЌЕНЕуBЕФОрРыDBЪЧ2ЃЌФЧУДЕуDОЭВЛЪЧЃЈAЃЌB)ЕФКУЕуЃЌЕЋЕуDЪЧЃЈBЃЌA)ЕФКУЕу.
ЃЈжЊЪЖдЫгУЃЉЃКЃЈ1)ШчЭМ1ЃЌБэЪОЪ§______КЭ_______ЕФЕуЪЧЃЈAЃЌBЃЉЕФКУЕуЃЛ

ЃЈ2)ШчЭМ2ЃЌMЁЂNЮЊЪ§жсЩЯСНЕуЃЌЕуMЫљБэЪОЕФЪ§ЮЊЃ2ЃЌЕуNЫљБэЪОЕФЪ§ЮЊ4.

ЂйБэЪОЪ§______ЕФЕуЪЧЃЈMЃЌN)ЕФКУЕуЃЛ
ЂкБэЪОЪ§______ЕФЕуЪЧЃЈNЃЌM)ЕФКУЕуЃЛ
(3)ШчЭМ3ЃЌAЁЂBЮЊЪ§жсЩЯСНЕуЃЌЕуAЫљБэЪОЕФЪ§ЮЊЃ20ЃЌЕуBЫљБэЪОЕФЪ§ЮЊ40.ЯжгавЛжЛЕчзгТьвЯPДгЕуBГіЗЂЃЌвд2ИіЕЅЮЛУПУыЕФЫйЖШЯђзѓдЫЖЏ.ЕБtЮЊКЮжЕЪБЃЌPЁЂAКЭBжаЧЁгавЛИіЕуЮЊЦфгрСНЕуЕФКУЕу?
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЖўДЮКЏЪ§y=ax2+bx+4ЕФЭМЯѓгыxжсНЛгкСНЕуAЁЂBЃЌгыyжсНЛгкЕуCЃЌЧвAЃЈЉ1ЃЌ0ЃЉЁЂBЃЈ4ЃЌ0ЃЉЃЎ
ЃЈ1ЃЉЧѓДЫЖўДЮКЏЪ§ЕФБэДяЪНЃЛ
ЃЈ2ЃЉШчЭМ1ЃЌХзЮяЯпЕФЖдГЦжсmгыxжсНЛгкЕуEЃЌCDЁЭmЃЌДЙзуЮЊDЃЌЕуFЃЈЉ![]() ЃЌ0ЃЉЃЌЖЏЕуNдкЯпЖЮDEЩЯдЫЖЏЃЌСЌНгCFЁЂCNЁЂFNЃЌШєвдЕуCЁЂDЁЂNЮЊЖЅЕуЕФШ§НЧаЮгыЁїFENЯрЫЦЃЌЧѓЕуNЕФзјБъЃЛ
ЃЌ0ЃЉЃЌЖЏЕуNдкЯпЖЮDEЩЯдЫЖЏЃЌСЌНгCFЁЂCNЁЂFNЃЌШєвдЕуCЁЂDЁЂNЮЊЖЅЕуЕФШ§НЧаЮгыЁїFENЯрЫЦЃЌЧѓЕуNЕФзјБъЃЛ
ЃЈ3ЃЉШчЭМ2ЃЌЕуMдкХзЮяЯпЩЯЃЌЧвЕуMЕФКсзјБъЪЧ1ЃЌНЋЩфЯпMAШЦЕуMФцЪБеыа§зЊ45ЁуЃЌНЛХзЮяЯпгкЕуPЃЌЧѓЕуPЕФзјБъЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌABЮЊжБОЖЃЌAB=4ЃЌCЁЂDЮЊдВЩЯСНИіЖЏЕуЃЌNЮЊCDжаЕуЃЌCMЁЭABгкMЃЌЕБCЁЂDдкдВЩЯдЫЖЏЪББЃГжЁЯCMN=30ЁуЃЌдђCDЕФГЄЃЈЁЁ ЃЉ
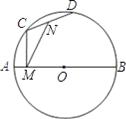
A. ЫцCЁЂDЕФдЫЖЏЮЛжУЖјБфЛЏЃЌЧвзюДѓжЕЮЊ4 B. ЫцCЁЂDЕФдЫЖЏЮЛжУЖјБфЛЏЃЌЧвзюаЁжЕЮЊ2
C. ЫцCЁЂDЕФдЫЖЏЮЛжУГЄЖШБЃГжВЛБфЃЌЕШгк2 D. ЫцCЁЂDЕФдЫЖЏЮЛжУЖјБфЛЏЃЌУЛгазюжЕ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЕу![]() КЭжБЯп
КЭжБЯп![]() ЃЈ
ЃЈ![]() ВЛЭЌЪБЮЊ0ЃЉЃЌдђЕу
ВЛЭЌЪБЮЊ0ЃЉЃЌдђЕу![]() ЕНжБЯп
ЕНжБЯп![]() ЕФОрРы
ЕФОрРы![]() ПЩгУЙЋЪН
ПЩгУЙЋЪН![]() МЦЫу.
МЦЫу.
Р§Шч.ЧѓЕу![]() ЕНжБЯп
ЕНжБЯп![]() ЕФОрРы.
ЕФОрРы.
НтЃКгЩжБЯпПЩжЊ![]()
Ёр![]()
ИљОнвдЩЯВФСЯЃЌНтД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉ ЧѓЕу![]() ЕНжБЯп
ЕНжБЯп![]() ЕФОрРыЃЛ
ЕФОрРыЃЛ
ЃЈ2ЃЉ ЧѓЕу![]() ЕНжБЯп
ЕНжБЯп![]() ЕФОрРыЃЌВЂЫЕУїЕу
ЕФОрРыЃЌВЂЫЕУїЕу![]() гыжБЯпЕФЮЛжУЙиЯЕЃЛ
гыжБЯпЕФЮЛжУЙиЯЕЃЛ
ЃЈ3ЃЉвбжЊжБЯп![]() гыжБЯп
гыжБЯп![]() ЦНааЃЌЧѓСНЬѕЦНааЯпМфЕФОрРы.
ЦНааЃЌЧѓСНЬѕЦНааЯпМфЕФОрРы.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
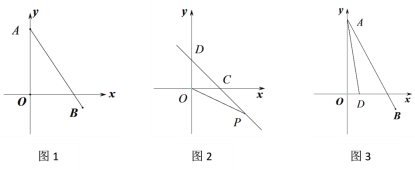
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌвбжЊAЃЈ0ЃЌ5ЃЉЃЌ BЃЈaЃЌbЃЉЃЌЧвaЃЌbТњзуbЃН![]() ЃЋ
ЃЋ![]() Ѓ1ЃЎ
Ѓ1ЃЎ
(1)ШчЭМЃЌЧѓЯпЖЮABЕФГЄЃЛ
(2)ШчЭМЃЌжБЯпCDгыxжсЁЂyжсе§АыжсЗжБ№НЛгкЕуCЃЌDЃЌЁЯOCDЃН45ЁуЃЌЕкЫФЯѓЯоЕФЕуPЃЈmЃЌnЃЉдкжБЯпCDЩЯЃЌЧвmnЃНЃ6ЃЌЧѓOP2ЃOC2ЕФжЕЃЛ
(3)ШчЭМЃЌШєЕуDЃЈ1ЃЌ0ЃЉЃЌЧѓЁЯDAO ЃЋЁЯBAOЕФЖШЪ§.
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com