Question

14．[问题情境]
将一副直角三角板（Rt△ABC和Rt△DEF）按如图1所示的方式摆放，其中∠ACB=90°，CA=CB，∠FDE=90°，O是AB的中点，点D与点O重合，DF⊥AC于点M，DE⊥BC于点N，连接MN，试判断△OMN与△CBA是否相似，并说明理由．

[探究展示]
小明同学展示如下正确的解法：
解：△OMN∽△CBA，证明如下：
∵CA=CB，∴∠A=∠B．
∵O是AB的中点，∴OA=OB．
∵DF⊥AC于点M，DE⊥BC于点N，∴∠AMO=∠BNO=90°．
∵在△OMA与△ONB中，$\left\{\begin{array}{l}{∠AMO=∠BNO}\\{∠A=∠B}\\{OA=OB}\end{array}\right.$
∴△OMA≌△ONB（依据1）．
∴OM=ON．
∵CA=CB，∴$\frac{OM}{CA}$=$\frac{ON}{CB}$．
又∵∠MON=∠ACB，
∴△OMN∽△CBA（依据2）．
[反思交流]
（1）上述证明过程中的“依据1”和“依据2”分别指的是什么？
依据1：AAS；
依据2：两组对应边成比例且夹角相等的两个三角形相似．
（2）将图1中的Rt△DEF沿着射线BA的方向平移，使点D落在BA的延长线上，FD的延长线与CA的延长线垂直相交于点M，BC的延长线与DE垂直相交于点N，连接OM，ON，MN，如图2所示，试判断△OMN的形状，并注明你的结论；
（3）将图1中的Rt△DEF沿着射线AB的方向平移，使点D落在AB的延长线上，直线FD与直线CA垂直相交于点M，直线BC与直线DE垂直相交于点N，连接OM，ON，MN，如图3所示，试判断△OMN的形状，并注明你的结论．

Answer 1

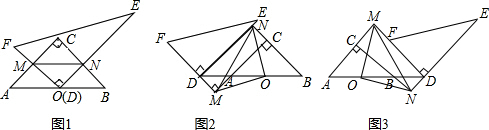
分析 （1）根据全等三角形的判定定理和相似三角形的判定定理即可得到结论；
（2）如图2，连接OC，由∠ACB=∠DNB，∠B=∠B，于是推出△BCA∽△BND，根据相似三角形的性质得到$\frac{AC}{DN}=\frac{BC}{BN}$，推出∠NCM=90°=∠DNC，根据平行线的性质得到∠DMC=90°，证得四边形DMCN是矩形，根据矩形的性质得到DN=MC，根据三角形的内角和得到∠3=∠B=45°，证得DN=NB，求出MC=NB，推出∠1=∠2=45°=∠B，OC=OB（斜边中线等于斜边一半），得到△MOC≌△NOB（SAS），根据全等三角形的性质得到OM=ON，∠MOC=∠NOB，于是得到∠MOC-∠CON=∠NOB-∠CON，即可得到结论；（3）如图3，连接OC，根据已知条件推出四边形MDNC是矩形，根据矩形的性质得到CM=ND，根据三角形的内角和得到∠ADN=45°，于是得到∠ADN=∠DBN，由等腰三角形判定得到DN=BN，推出CM=BN，根据邻补角的定义得到∠MCO=135°，于是得到∠MCO=∠OBN，推出△OMC≌△ONB，根据全等三角形的性质得到∠COM=∠BON，OM=ON，由∠COB=90°，于是得到∠MOB+∠NOB=90°，即可得到结论．

解答 解：（1）依据1：AAS；
依据2：两组对应边成比例且夹角相等的两个三角形相似；
故答案为：AAS，两组对应边成比例且夹角相等的两个三角形相似．

（2）△OMN是等腰直角三角形，如图2，连接OC，
∵∠ACB=∠DNB，∠B=∠B，
∴△BCA∽△BND，
∴$\frac{AC}{DN}=\frac{BC}{BN}$，
∵AC=BC，
∴DN=NB．
∵∠ACB=90°，
∴∠NCM=90°=∠DNC，
∴MC∥DN，
又∵DF⊥AC，
∴∠DMC=90°，
即∠DMC=∠MCN=∠DNC=90°，
∴四边形DMCN是矩形，
∴DN=MC，
∵∠B=45°，∠DNB=90°，
∴∠3=∠B=45°，
∴DN=NB，
∴MC=NB，
∵∠ACB=90°，O为AB中点，AC=BC，
∴∠1=∠2=45°=∠B，OC=OB（斜边中线等于斜边一半），
在△MOC和△NOB中，
$\left\{\begin{array}{l}{OC=OB}\\{∠1=∠2}\\{CM=BN}\end{array}\right.$，
∴△MOC≌△NOB（SAS），
∴OM=ON，∠MOC=∠NOB，
∴∠MOC-∠CON=∠NOB-∠CON，
即∠MON=∠BOC=90°，
∴OM⊥ON，
∴△OMN是等腰直角三角形；

（3）△OMN是等腰直角三角形；
证明：如图3，连接OC，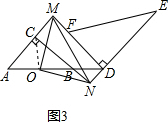
∵O是AB的中点，
∴OC=BO，OC⊥OB，
∵∠DMC=∠MDN=∠CND=90°，
∴四边形MDNC是矩形，
∴CM=ND，
∵∠NBD=∠CBA=45°，∠BND=90°，
∴∠ADN=45°，
∴∠ADN=∠DBN，
∴DN=BN，
∴CM=BN，
∵∠OCA+∠MCO=180°，∠ACO=45°，
∴∠MCO=135°，
∴∠MCO=∠OBN，
在△OMC与△ONB中，$\left\{\begin{array}{l}{CM=NB}\\{∠MCO=∠OBN}\\{OC=OB}\end{array}\right.$，
∴△OMC≌△ONB，
∴∠COM=∠BON，OM=ON，
∵∠COB=90°，
即∠MOC+∠MOB=90°，
∴∠MOB+∠NOB=90°，
即∠NOM=90°，
∴△OMN是等腰直角三角形．

点评 本题考查了等腰三角形的性质和判定，全等三角形的性质和判定，矩形的性质和判定，角平分线性质等知识点的应用，主要考查学生运用定理进行推理的能力，题目比较好，综合性也比较强．