
分析 (1)只需令根的判别式等于0,就可解决问题;
(2)①若a为底边,则b=c,则有根的判别式等于0,即可求出m的值,然后代入原方程,并解此方程,由此可求出△ABC的周长;②若a为腰,则b=a=3,或c=a=3,则原方程有一根为3,把x=3代入方程,求出m,然后解此方程,由此可求出△ABC的周长.
解答 解:(1)∵方程有两个相等的实数根,
∴△=m2-4×1×(2-$\frac{1}{2}$m)=0,
解得:m1=-4,m2=2;
(2)①若a为底边,则b=c,
∴△=m2-4×1×(2-$\frac{1}{2}$m)=0,
解得:m1=-4,m2=2;
当m=-4时,原方程为x2-4x+4=0,
解得x1=x2=2,
∵2+2>3,
∴2、2、3能构成三角形,
此时△ABC的周长为2+2+3=7;
当m=2时,原方程为x2+2x+1=0,
解得x=-1(舍去)
②若a为腰,则b=a=3,或c=a=3,
32+3m+2-$\frac{1}{2}$m=0,
解得m=-$\frac{22}{5}$,
此时原方程为x2-$\frac{22}{5}$x+$\frac{21}{5}$=0,
解得x1=$\frac{7}{5}$,x2=3,
∵3+3>$\frac{7}{5}$,
∴3、3、$\frac{7}{5}$能构成三角形,
此时△ABC的周长为3+3+$\frac{7}{5}$=$\frac{37}{5}$;
综上所述:△ABC的周长为7或$\frac{37}{5}$.
点评 本题主要考查了根的判别式、等腰三角形的性质、解一元二次方程、三角形的构成条件等知识,运用分类讨论的思想是解决本题的关键,需要注意的是,涉及到三角形的三边时,要考虑三角形的构成条件.


科目:初中数学 来源: 题型:解答题
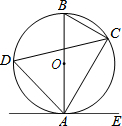 如图,已知AB是⊙O的直径,点C、D在⊙O上,点E在⊙O外,∠EAC=∠D=60°.
如图,已知AB是⊙O的直径,点C、D在⊙O上,点E在⊙O外,∠EAC=∠D=60°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
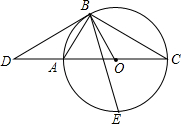 如图,AC为⊙O的直径,D为CA延长线上一点,AB=AD=A0,点B在⊙O上,
如图,AC为⊙O的直径,D为CA延长线上一点,AB=AD=A0,点B在⊙O上,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
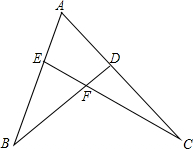 已知,如图,点D、E分别在AC、AB上,BD、CE交于F,∠B:∠C=3:2.
已知,如图,点D、E分别在AC、AB上,BD、CE交于F,∠B:∠C=3:2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 为了方便行人,市政府打算修建如图所示的过街天桥,桥面AD平行于地面BC,立柱AE⊥BC于点E,立柱DF⊥BC于点F,若AB=10$\sqrt{5}$米,tanB=$\frac{1}{2}$,∠C=30°.
为了方便行人,市政府打算修建如图所示的过街天桥,桥面AD平行于地面BC,立柱AE⊥BC于点E,立柱DF⊥BC于点F,若AB=10$\sqrt{5}$米,tanB=$\frac{1}{2}$,∠C=30°.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com