
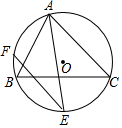
 如图,在△ABC中,∠BAC的平分线和它的外接圆⊙O相交于点E,过E作弦EF,使EF=AB.求证:EF∥AC.
如图,在△ABC中,∠BAC的平分线和它的外接圆⊙O相交于点E,过E作弦EF,使EF=AB.求证:EF∥AC. 分析 先根据圆心角、弧、弦的关系由EF=AC得到$\widehat{EF}$=$\widehat{AB}$,则$\widehat{AF}$=$\widehat{BE}$,再根据圆周角定理得∠E=∠EAC,由于∠BAE=∠EAC,所以∠E=∠BAE,然后根据平行线的判定即可得到EF∥AB.
解答 证明:∵ EF=AB,
EF=AB,
∴$\widehat{EF}$=$\widehat{AB}$,
∴$\widehat{BF}$+$\widehat{BE}$=$\widehat{BF}$+$\widehat{AF}$,
∴$\widehat{AF}$=$\widehat{BF}$,
∴∠EAB=∠AEF,
∵∠BAE=∠CAE,
∴∠CAE=∠AEF,
∴EF∥AC.
点评 本题考查了圆心角、弧、弦的关系:在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等.也考查了圆周角定理.


 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com