
科目:初中数学 来源: 题型:
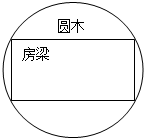 如图,有一种房梁的截面是一个矩形,且矩形的长与宽之比为
如图,有一种房梁的截面是一个矩形,且矩形的长与宽之比为| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
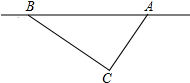 2011年第一季度,我国南方多省市遭遇特大干旱,为了抗旱保收,某市准备开采地下水,经探测2012-01-03 18:36C处地下有水,为此C处需要爆破,已知C处与公路上的停靠站A的距离是300m,与公路上另一停靠站B的距离为400m,且CA垂直CB,为了安全,爆破点C周围250m的范围内禁止进入.问:在进行爆破时,公路AB段是否有危险,是否需要暂时封锁?
2011年第一季度,我国南方多省市遭遇特大干旱,为了抗旱保收,某市准备开采地下水,经探测2012-01-03 18:36C处地下有水,为此C处需要爆破,已知C处与公路上的停靠站A的距离是300m,与公路上另一停靠站B的距离为400m,且CA垂直CB,为了安全,爆破点C周围250m的范围内禁止进入.问:在进行爆破时,公路AB段是否有危险,是否需要暂时封锁?查看答案和解析>>
科目:初中数学 来源: 题型:
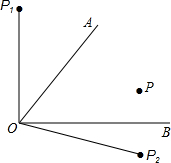 如图,点P是∠AOB内部的一定点.
如图,点P是∠AOB内部的一定点.查看答案和解析>>
科目:初中数学 来源: 题型:
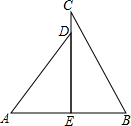 两个直角三角形按如图方式摆放,若AD=10,BE=6,∠ADE=37°,∠BCE=29°.求CD长(精确到0.01).
两个直角三角形按如图方式摆放,若AD=10,BE=6,∠ADE=37°,∠BCE=29°.求CD长(精确到0.01).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com