
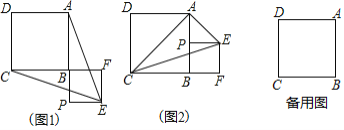
【题目】已知正方形ABCD,P为射线AB上的一点,以BP为边作正方形BPEF,使点F在线段CB的延长线上,连接EA、EC.
(1)如图1,若点P在线段AB的延长线上,求证:EA=EC;
(2)若点P在线段AB上,如图2,当点P为AB的中点时,判断△ACE的形状,并说明理由;
(3)在(1)的条件下,将正方形ABCD固定,正方形BPEF绕点B旋转一周,设AB=4,BP=a,若在旋转过程中△ACE面积的最小值为4,请直接写出a的值.
【答案】(1)见解析;(2)△ACE是直角三角形,理由见解析;(3)a=1.
【解析】
(1)根据正方形的性质和全等三角形的判定定理证明△APE≌△CFE,根据全等三角形的性质证明结论;
(2)根据正方形的性质、等腰直角三角形的性质解答;
(3)连接BD、AC交于点O.点E的运动轨迹是以B为圆心,![]() a为半径的圆,则当点E在对角线BD上时,△ACE的面积最小, 根据
a为半径的圆,则当点E在对角线BD上时,△ACE的面积最小, 根据![]() ×AC×OE=4,得到OE=
×AC×OE=4,得到OE=![]() ,即可求出BE=2
,即可求出BE=2![]() –
–![]() =
=![]() ,进而求出 a=1.
,进而求出 a=1.
(1)如图1中,
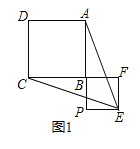
∵四边形ABCD和四边形BPEF是正方形,
∴AB=BC,BP=BF,∴AP=CF,
在△APE和△CFE中,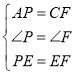 ,
,
∴△APE≌△CFE,
∴EA=EC;
(2)△ACE是直角三角形,
理由如下:如图2中,
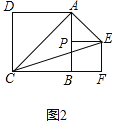
∵P为AB的中点,∴PA=PB,
∵PB=PE,∴PA=PE,∴∠PAE=45°,
又∵∠BAC=45°,
∴∠CAE=90°,即△ACE是直角三角形;
(3)如图3,连接BD、AC交于点O.
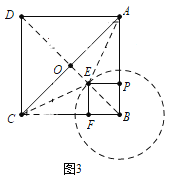
∵点E的运动轨迹是以B为圆心,![]() a为半径的圆,
a为半径的圆,
∴当点E在对角线BD上时,△ACE的面积最小,
∵![]() ×AC×OE=4,∴OE=
×AC×OE=4,∴OE=![]() ,
,
∵BE=2![]() –
–![]() =
=![]() ,∴a=1.
,∴a=1.


科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,BC>AB>AC.甲、乙两人想在BC上取一点P,使得∠APC=2∠ABC,其作法如下:
(甲)作AB的中垂线,交BC于P点,则P即为所求;
(乙)以B为圆心,AB长为半径画弧,交BC于P点,则P即为所求.
对于两人的作法,下列判断何者正确?( )
![]()
A. 两人皆正确B. 两人皆错误C. 甲正确,乙错误D. 甲错误,乙正确
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】周老师为了了解学生自主学习、合作交流的具体情况,对本班部分学生进行了为期半年的跟踪调查,并将调查结果分成四类A:优;B:良;C:中;D:差.依据调查结果绘制成以下两幅不完整的统计图,请你根据统计图解答下列问题:
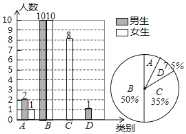
(1)本次调查中,周老师一共调查了______名学生;
(2)将统计图补充完整;
(3)为了共同进步,周老师想从被调查的A类和D类学生中分别选取一位同学进行“一对一”帮扶,请用列表法或画树形图的方法求所选的两位同学恰好是两位女同学的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,△BPC是等边三角形,BP、CP的延长线分别交AD于点E、F,连接BD、DP,BD与CF相交于点H,给出下列结论:①BE=2AE;②△DFP∽△BPH;③△PFD∽△PDB;④DP2=PHPC
其中正确的是( )

A. ①②③④ B. ②③ C. ①②④ D. ①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,抛物线![]() 与x轴交于A、B两点(点A在x轴的负半轴),与y轴交于点C
与x轴交于A、B两点(点A在x轴的负半轴),与y轴交于点C![]() . 抛物线的对称轴交抛物线于点D,交x轴于点E,点P是线段DE上一动点(点P不与DE两端点重合),连接PC、PO.
. 抛物线的对称轴交抛物线于点D,交x轴于点E,点P是线段DE上一动点(点P不与DE两端点重合),连接PC、PO.
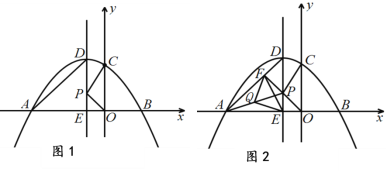
(1) 求抛物线的解析式和对称轴;
(2) 求∠DAO的度数和△PCO的面积;
(3) 在图1中,连接PA,点Q 是PA 的中点.过点P作PF⊥AD于点F,连接QE、QF、EF得到图2.试探究: 是否存在点P,使得![]() ,若存在,请求点P的坐标;若不存在,请说明理由.
,若存在,请求点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】等腰三角形的屋顶,是建筑中经常采用的结构形式.在如图所示的等腰三角形屋顶ABC中,AB=AC,测得BC=20米,∠C=41°,求顶点A到BC边的距离是多少米?(结果精确到0.1米.参考数据:sin41°≈0.656,cos41°≈0.755,tan41°≈0.869.)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com