
【题目】如图,在平面直角坐标系内,正方形ABCD中的顶点B,D的坐标分别是(0,0),(2,0),且A,C两点关于x轴对称,则C点对应的坐标是( )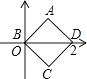
A.(1,1)
B.(1,﹣1)
C.(1,﹣2)
D.(2,﹣2)
科目:初中数学 来源: 题型:
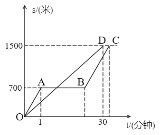
【题目】“龟兔赛跑”的故事同学们都听过,图中的线段OD和折线OABC表示龟兔赛跑时路程与时间的关系,请根据图中的信息,解决下列问题:
(1)填空:折线OABC表示赛跑过程中_________(填“兔子”或“乌龟”)的路程与时间的关系,赛跑的全程是_______米.
(2)兔子在起初每分钟跑多少米?乌龟每分钟爬多少米?
(3)乌龟用了多少分钟追上了正在睡觉的兔子?
(4)兔子醒来后以400米/分钟的速度跑向终点,结果还是比乌龟晚到了0.5分钟,请你算算兔子中间停下睡觉用了多少时间?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题中真命题的个数是( )
①平面内,过一点有且只有一条直线与已知直线平行;②![]() 这5个数中有2个是无理数;③若
这5个数中有2个是无理数;③若![]() ,则点P(-m,5)在第一象限;④
,则点P(-m,5)在第一象限;④![]() 的算术平方根是4;⑤经过一点有且只有一条直线与已知直线垂直;⑥同旁内角互补.
的算术平方根是4;⑤经过一点有且只有一条直线与已知直线垂直;⑥同旁内角互补.
A.2B.3C.4D.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】芜湖长江大桥是中国跨度最大的公路和铁路两用桥梁,大桥采用低塔斜拉桥桥型(如甲图),图乙是从图甲引申出的平面图,假设你站在桥上测得拉索AB与水平桥面的夹角是30°,拉索CD与水平桥面的夹角是60°,两拉索顶端的距离BC为2米,两拉索底端距离AD为20米,请求出立柱BH的长.(结果精确到0.1米, ![]() ≈1.732)
≈1.732)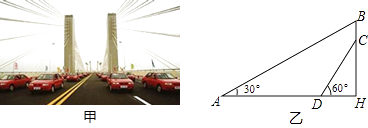
查看答案和解析>>
科目:初中数学 来源: 题型:
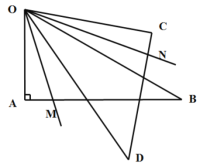
【题目】如图,直线y=﹣x+1与x轴,y轴分别交于B,A两点,动点P在线段AB上移动,以P为顶点作∠OPQ=45°交x轴于点Q.

(1)求点A和点B的坐标;
(2)比较∠AOP与∠BPQ的大小,说明理由.
(3)是否存在点P,使得△OPQ是等腰三角形?若存在,请求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】作图题:如图,在平面直角坐标系![]() 中,
中,![]() ,
,![]() ,
,![]()

(1)画出![]() 的
的![]() 边上的高CH;
边上的高CH;
(2)将![]() 平移到
平移到![]() (点
(点![]() 和点
和点![]() 对应,点
对应,点![]() 和点
和点![]() 对应,点
对应,点![]() 和点
和点![]() 对应),若点
对应),若点![]() 的坐标为
的坐标为![]() ,请画出平移后的
,请画出平移后的![]() ;
;
(3)若![]() ,
,![]() 为平面内一点,且满足
为平面内一点,且满足![]() 与
与![]() 全等,请直接写出点
全等,请直接写出点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,∠B=90°,AB∥CD,M为BC边上的一点,且AM平分∠BAD,DM平分∠ADC.
求证:(1)AM⊥DM;
(2)M为BC的中点.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将一副三角板如图摆放,∠OAB=∠OCD=90°,∠AOB=60°,∠COD=45°,OM平分∠AOD,ON平分∠COB,则∠MON的度数为( )
A.60°B.45°C.65.5°D.52.5°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在直角梯形ABCD中,![]() ,
,![]() ,
,![]() ,
,![]() .
.
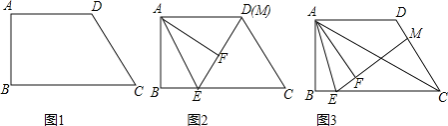
(1)如图1,连接AC,求证:CA是![]() 的平分线;
的平分线;
(2)线段BC上一点E,将![]() 沿AE翻折,点B落到点F处,射线EF与线段CD交于点M.
沿AE翻折,点B落到点F处,射线EF与线段CD交于点M.
①如图2,当点M与点D重合时,求证:![]() ;
;
②如图3,当点M不与点D重合时,求证:![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com