Question

13．如图，已知一次函数y=x-1的图象与x轴、y轴分别交于点A、B，点P是y轴上的任意一点，点C是一次函数y=x-1图象上的任意一点，且点C位于第一象限，
（1）求A、B两点的坐标；
（2）过点C作CD⊥x轴，垂足为D，连接PA、PC，若PA=PC，求证：（PO-CD）是一个定值；
（3）若以点P、A、C为顶点的三角形是等腰直角三角形，求点P的坐标．（提示：作答时可利用备用图画示意图）

Answer 1

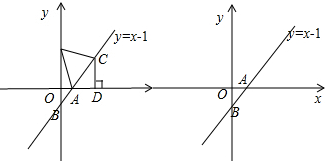
分析 （1）根据自变量与函数值的对应关系，可得A、B点坐标；
（2）根据PA与PC的关系，可得关于x的方程，根据解方程，可得x的值，根据整式的加减，可得答案；
（3）分类讨论：AP=PC，根据AB与坐标轴的交点，可得答案；
PA=AC，可得AP与AC的关系，可得AP的解析式，根据自变量与函数值的对应关系，可得P点坐标；
AC=PC，可得PA平行于y轴，可得P不在y轴上．

解答 解：（1）当y=0时，x-1=0，解得x=1，即A（1，0）；
当x=0时，y=-1，即B（0，-1）；
（2）证明：设P（0，a），C（x，x-1），
由PA=PC，得
1+a²=x²+（a-x+1）²，
化简，得
x²-（a+1）x+a=0，
解得x=1（不符合题意的解要舍去），x=a，
C（a，a-1）．
PO-CD=a-（a-1）=1，
∴PO-CD是定值；
（3）如图1：，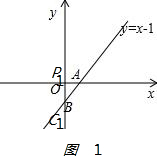
①PA=PC且∠PCA=45°，
C与B重合，P与O重合，即P₁（0，0）（C在第一象限，舍）；
②如图2：，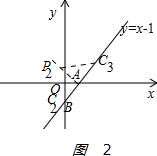
PA=AC时，∠PAC=90°，直线PA的解析式为y=-x+b，
将A点坐标代入，得-1+b=0，
解得b=1，
即PB的解析式为y=-x+1，
当x=0时，y=1，即P₂（0，1），
③如图3：，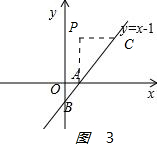
PC=AC时，∠PAC=45°，∠CAD=45°，
∠PAD=∠PAC+∠CAD=90°，
即PA⊥x轴，P不在y轴上，P点不存在，
综上所述：点P、A、C为顶点的三角形是等腰直角三角形，点P的坐标（0，1）．

点评 本题考查了一次函数综合题，（1）利用了自变量与函数值的对应关系是求直线与坐标轴交点的关键；（2）利用勾股定理的出关于X的方程是解题关键；利用等腰直角三角形的判定，分类讨论是解题关键，以防遗漏．