
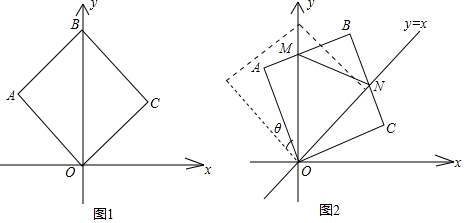
分析 (1)由题意当点A落到y轴正半轴上时,边BC在旋转过程中所扫过的面积=S扇形OBB′+S△OCB′-S△OBC-S扇形OCC′由此计算即可.
(2)如图2中,在OA取一点E,使得EM=EO,首先证明△AEM是等腰直角三角形,推出AM=AE,设AE=AM=x,则EM=EO=$\sqrt{2}$x,可得x+$\sqrt{2}$x=1,解得x=$\sqrt{2}$-1,推出BM=AB-AM=1-($\sqrt{2}$-1)=2-$\sqrt{2}$,同理可得BN=2-$\sqrt{2}$,推出MN=$\sqrt{2}$BM=2$\sqrt{2}$-2,设△BMN的内切圆的半径为r,则有$\frac{1}{2}$(MN+BM+BN)•r=$\frac{1}{2}$BM•BN,由此求出r即可解决问题.
(3)在正方形OABC旋转的过程中l值不发生变化.如图3中,延长BA到E使得AE=CN.只要证明△OAE≌△OCN,推出OE=ON,∠AOE=∠CON,再证明△MOA≌△MON,推出EM=MN,推出△BNM的周长=MN+BM+BN=EM+BM+BN=(AM+BM)+(AE+BN)=(AM+BM)+(CN+BN)=2AB=2.
解答 解:(1)如图1中,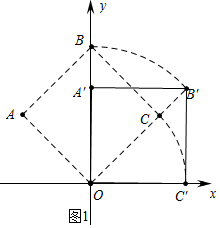
由题意当点A落到y轴正半轴上时,边BC在旋转过程中所扫过的面积=S扇形OBB′+S△OCB′-S△OBC-S扇形OCC′
=S扇形OBB′-S扇形OCC′
=$\frac{45•π•(\sqrt{2})^{2}}{360}$-$\frac{45•π•{1}^{2}}{360}$
=$\frac{π}{8}$.
(2)如图2中,在OA取一点E,使得EM=EO,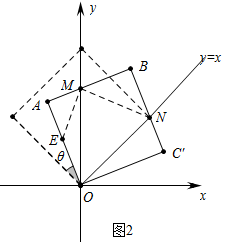
∵∠AOM=22.5°,
∴∠EOM=∠EMO=22.5°,
∴∠AEM=∠EOM+∠EMO=45°,
∴△AEM是等腰直角三角形,
∴AM=AE,设AE=AM=x,则EM=EO=$\sqrt{2}$x,
∴x+$\sqrt{2}$x=1,
∴x=$\sqrt{2}$-1,
∴BM=AB-AM=1-($\sqrt{2}$-1)=2-$\sqrt{2}$,同理可得BN=2-$\sqrt{2}$,
∴MN=$\sqrt{2}$BM=2$\sqrt{2}$-2,
设△BMN的内切圆的半径为r,
则有$\frac{1}{2}$(MN+BM+BN)•r=$\frac{1}{2}$BM•BN,
∴r=$\frac{BM•BN}{MN+BM+BN}$=$\frac{(2-\sqrt{2})^{2}}{2\sqrt{2}-2+2-\sqrt{2}+2-\sqrt{2}}$=3-2$\sqrt{2}$.
(3)在正方形OABC旋转的过程中l值不发生变化.
理由:如图3中,延长BA到E使得AE=CN.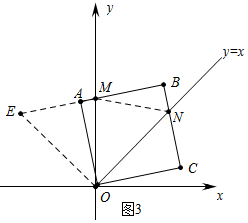
∵AE=CN,∠OAE=∠OCN=90°,OA=OC,
∴△OAE≌△OCN,
∴OE=ON,∠AOE=∠CON,
∵∠MON=45°,
∴∠MOA+∠CON=∠MOA+∠AOE=45°,
∴∠MOE=∠MON,∵OM=OM,
∴△MOA≌△MON,
∴EM=MN,
∴△BNM的周长=MN+BM+BN=EM+BM+BN
=(AM+BM)+(AE+BN)=(AM+BM)+(CN+BN)=2AB=2,
∴△BNM的周长为定值.
点评 本题考查圆综合题、正方形的性质、全等三角形的判定和性质、三角形的内切圆、等腰直角三角形的性质和判定、勾股定理等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,属于中考压轴题.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
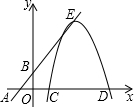 如图,一次函数y=x+2与x轴交于点A,与y轴交于点B,一抛物线的顶点在直线AB上,形状与函数y=-$\frac{1}{2}$x2图象相同,它与x轴分别交于点C、D(点C在点D的左侧),抛物线的顶点为点E.
如图,一次函数y=x+2与x轴交于点A,与y轴交于点B,一抛物线的顶点在直线AB上,形状与函数y=-$\frac{1}{2}$x2图象相同,它与x轴分别交于点C、D(点C在点D的左侧),抛物线的顶点为点E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
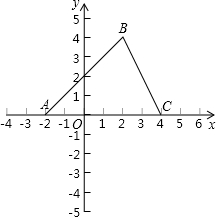 如图,在直角坐标系中,△ABC的顶点A(-2,0),B(2,4),C(4,0).
如图,在直角坐标系中,△ABC的顶点A(-2,0),B(2,4),C(4,0).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (a+b)(b-a)=a2-b2 | B. | (a-b)2=a2-b2 | ||
| C. | (2x-y)2=4x2-2xy+y2 | D. | (x-2y)(-2y-x)=4y2-x2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com