
【题目】如图,已知⊙O的半径为2,AB为直径,CD为弦.AB与CD交于点M,将 ![]() 沿CD翻折后,点A与圆心O重合,延长OA至P,使AP=OA,连接PC
沿CD翻折后,点A与圆心O重合,延长OA至P,使AP=OA,连接PC
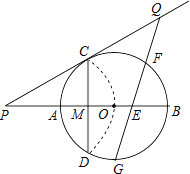
(1)求CD的长;
(2)求证:PC是⊙O的切线;
(3)点G为 ![]() 的中点,在PC延长线上有一动点Q,连接QG交AB于点E.交
的中点,在PC延长线上有一动点Q,连接QG交AB于点E.交 ![]() 于点F(F与B、C不重合).问GEGF是否为定值?如果是,求出该定值;如果不是,请说明理由.
于点F(F与B、C不重合).问GEGF是否为定值?如果是,求出该定值;如果不是,请说明理由.
【答案】(1)2![]() ;(2)见解析;(3)见解析.
;(2)见解析;(3)见解析.
【解析】试题(1)连接OC,根据翻折的性质求出OM,CD⊥OA,再利用勾股定理列式求解即可;
(2)利用勾股定理列式求出PC,然后利用勾股定理逆定理求出∠PCO=90°,再根据圆的切线的定义证明即可;
(3)连接GA、AF、GB,根据等弧所对的圆周角相等可得∠BAG=∠AFG,然后根据两组角对应相等两三角相似求出△AGE和△FGA相似,根据相似三角形对应边成比例可得![]() ,从而得到GEGF=
,从而得到GEGF=![]() ,再根据等腰直角三角形的性质求解即可.
,再根据等腰直角三角形的性质求解即可.
试题解析:(1)解:如图,连接OC,∵![]() 沿CD翻折后,点A与圆心O重合,∴OM=
沿CD翻折后,点A与圆心O重合,∴OM=![]() OA=
OA=![]() ×2=1,CD⊥OA,∵OC=2,∴CD=2CM=
×2=1,CD⊥OA,∵OC=2,∴CD=2CM=![]() =
=![]() =
=![]() ;
;
(2)证明:∵PA=OA=2,AM=OM=1,CM=![]() CD=
CD=![]() ,∠CMP=∠OMC=90°,∴PC=
,∠CMP=∠OMC=90°,∴PC=![]() =
=![]() =
=![]() ,∵OC=2,PO=2+2=4,∴
,∵OC=2,PO=2+2=4,∴![]() =
=![]() =16=
=16=![]() ,∴∠PCO=90°,∴PC是⊙O的切线;
,∴∠PCO=90°,∴PC是⊙O的切线;
(3)解:GEGF是定值,证明如下:
如图,连接GA、AF、GB,∵点G为![]() 的中点,∴
的中点,∴![]() ,∴∠BAG=∠AFG,又∵∠AGE=∠FGA,∴△AGE∽△FGA,∴
,∴∠BAG=∠AFG,又∵∠AGE=∠FGA,∴△AGE∽△FGA,∴![]() ,∴GEGF=
,∴GEGF=![]() ,∵AB为直径,AB=4,∴∠BAG=∠ABG=45°,∴AG=
,∵AB为直径,AB=4,∴∠BAG=∠ABG=45°,∴AG=![]() ,∴GEGF=8.
,∴GEGF=8.



 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案科目:初中数学 来源: 题型:
【题目】2019年10月18日至27日(共10天)武汉军运会期间,从19日起武汉体育中心9天中接收观众人数的变化情况如下表(正数表示比前一天多的人数,负数表示经前一天少的人数):
日期 | 19日 | 20日 | 21日 | 2日 | 23日 | 24日 | 25日 | 26日 | 27日 |
人数变化/万人 | +0.5 | +0.7 | +0.8 | -0.4 | -0.6 | +0.2 | +0.3 | +0.5 | +0.2 |
(1)请判断这9天中,游客人数最多和最少的各是哪一天?它们相差多少万人?
(2)如果10月18日观众人数为2万人,平均每人门票100元,请问武汉体育中心在军运会这10天期间门票总收入为多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果一元一次方程的根是一元一次不等式组的解,则称该一元一次方程为该不等式组的关联方程
(1)在方程①3x﹣1=0,②x﹣(3x+1)=﹣7中,不等式组![]() 的关联方程是 ;(填序号)
的关联方程是 ;(填序号)
(2)若不等式组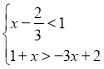 的一个关联方程的解是整数,则这个关联方程可以是 ;(写出一个即可)
的一个关联方程的解是整数,则这个关联方程可以是 ;(写出一个即可)
(3)若方程10﹣3x=2x,1+x=2(x﹣1)都是关于x的不等式组![]() 的关联方程,求出m的取值范围.
的关联方程,求出m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明从右边的二次函数y=ax2+bx+c图象中,观察得出了下面的五条信息:①a<0,②c=0,③函数的最小值为-3,④当x<0时,y>0,⑤当0<x1<x2<2时,y1>y2 , (6)对称轴是直线x=2.你认为其中正确的个数为( )
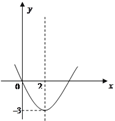
A. 2 B. 3 C. 4 D. 5
查看答案和解析>>
科目:初中数学 来源: 题型:
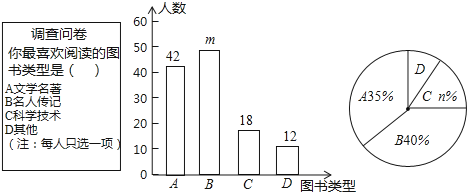
【题目】为了培养学生的阅读习惯,某校开展了“读好书,助成长”系列活动,并准备购置一批图书,购书前 ,对学生喜欢阅读的图书类型进行了抽样调查,并将调查数据绘制成两幅不完整的统计图,如图所示,根据统计图所提供的信息,回答下列问题:
(1)本次调查共抽查了 名学生,两幅统计图中的m= ,n= .
(2)已知该校共有960名学生,请估计该校喜欢阅读“A”类图书的学生约有多少人?
(3)学校要举办读书知识竞赛,七年(1)班要在班级优胜者2男1女中随机选送2人参赛,求选送的两名参赛学生为1男1女的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一家商店进行装修,若请甲、乙两个装修组同时施工,8天可以完成,需付两组费用共3520元,若先请甲组单独做6天,再请乙组单独做12天可以完成,需付费用3480元,问:
(1)甲,乙两组工作一天,商店各应付多少钱?
(2)已知甲单独完成需12天,乙单独完成需24天,单独请哪个组,商店所需费用最少?
(3)若装修完后,商店每天可贏利200元,你认为如何安排施工更有利于商店?请你帮助商店决策.(可用(1)(2)问的条件及结论)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O是△ABC的外接圆,AE平分∠BAC交⊙O于点E,交BC于点D,过点E做直线l∥BC.

(1)判断直线l与⊙O的位置关系,并说明理由;
(2)若∠ABC的平分线BF交AD于点F,求证:BE=EF;
(3)在(2)的条件下,若DE=4,DF=3,求AF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】科技改变世界.2017年底,快递分拣机器人从微博火到了朋友圈.据介绍,这些机器人不仅可以自动规划最优路线,将包裹准确地放入相应的路口,还会感应避让障碍物,自动归队取包裹,没电的时候还会自己找充电桩充电.某快递公司启用40台A种机器人、150台B种机器人分拣快递包裹,A、B两种机器人全部投入工作,1小时共可以分拣0.77万件包裹;若全部A种机器人工作1.5小时,全部B种机器人工作2小时,一共可以分拣1.38万件包裹.
(1)求两种机器人每台每小时各分拣多少件包裹?
(2)为进一步提高效率,快递公司计划再购进A、B两种机器人共100台.若要保证新购进的这批机器人每小时的总分拣量不少于5500件,求至少应购进A种机器人多少台?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com