
 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 打开电视机,正在播广告,是必然事件 | |
| B. | 在连续5次的数学测试中,两名同学的平均分相同,方差较大的同学数学成绩更稳定 | |
| C. | 某同学连续10次抛掷质量均匀的硬币,3次正面向上,因此正面向上的概率是30% | |
| D. | 从一个只装有白球的缸里摸出一个球,摸出的球是白球 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
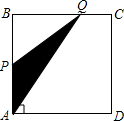 如图,四边形ABCD是矩形,AB=8,BC=4,动点P以每秒2个单位的速度从点A沿线段AB向B点运动,同时动点Q以每秒3个单位的速度从点B出发沿B-C-D的方向运动,当点Q到达点D时P、Q同时停止运动,若记△PQA的面积为y,运动时间为x,则下列图象中能大致表示y与x之间函数关系图象的是( )
如图,四边形ABCD是矩形,AB=8,BC=4,动点P以每秒2个单位的速度从点A沿线段AB向B点运动,同时动点Q以每秒3个单位的速度从点B出发沿B-C-D的方向运动,当点Q到达点D时P、Q同时停止运动,若记△PQA的面积为y,运动时间为x,则下列图象中能大致表示y与x之间函数关系图象的是( )| A. | 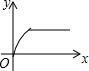 | B. | 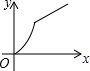 | C. |  | D. |  |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图:在△ABC中,AC=BC,点D、E分别是边AB、AC的中点,将△ADE绕点E旋转180°得△CFE,则四边形ADCF一定是( )
如图:在△ABC中,AC=BC,点D、E分别是边AB、AC的中点,将△ADE绕点E旋转180°得△CFE,则四边形ADCF一定是( )| A. | 矩形 | B. | 菱形 | C. | 正方形 | D. | 任意四边形 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
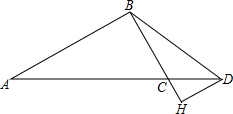 如图,在△ABC中,∠ABC=90°,BC=3,D为AC延长线上一点,AC=3CD,过点D作DH∥AB,交BC的延长线于点H.
如图,在△ABC中,∠ABC=90°,BC=3,D为AC延长线上一点,AC=3CD,过点D作DH∥AB,交BC的延长线于点H.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com