
分析 分别利用幂的乘方与积的乘方、零指数幂,负整数指数幂的知识进行计算后即可得到正确的结果.
解答 解:(-x2y)2=x4y2;
(-2)-2=$\frac{1}{(-2)^{2}}$=$\frac{1}{4}$;
-2x2•(-x)3=-2x2•(-x3)=2x5;
(-0.25)2014×42015=(-0.25)2014×42014×4=4.
(-1)2015+(-π)0+2-2=-1+1+$\frac{1}{4}$=$\frac{1}{4}$.
故答案为:x4y2、$\frac{1}{4}$、2x5、4、$\frac{1}{4}$.
点评 本题考查了幂的乘方与积的乘方、零指数幂,负整数指数幂的知识,解题的关键是熟练应用有关的幂的性质,难度不大.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 扩大5倍 | B. | 扩大10倍 | C. | 不变 | D. | 缩小$\frac{1}{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知:如图,△ABC中,∠C=90°,D为AB的中点,E、F分别在AC、BC上,且DE⊥DF.延长FD到G,使DG=DF,连结GE,GA.
已知:如图,△ABC中,∠C=90°,D为AB的中点,E、F分别在AC、BC上,且DE⊥DF.延长FD到G,使DG=DF,连结GE,GA.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
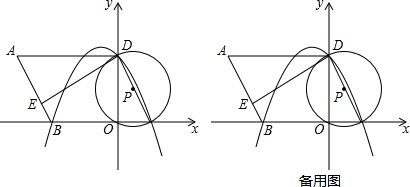
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com