
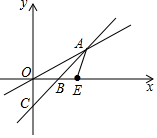
 如图,直线y=x-m与直线y=kx(k≠0)交于点A,直线y=x-m与x轴交于点B,与y轴交于点C,若直线y=kx(k≠0)与x轴正半轴所成夹角为30°,OB=$2({\sqrt{3}-1})$.
如图,直线y=x-m与直线y=kx(k≠0)交于点A,直线y=x-m与x轴交于点B,与y轴交于点C,若直线y=kx(k≠0)与x轴正半轴所成夹角为30°,OB=$2({\sqrt{3}-1})$.分析 (1)如图,作AF⊥OB于F.直线y=x-m与x轴交于点B,与y轴交于点C,可得B(m,0),C(0,-m),推出OC=OB,推出∠OBC=∠OCB=45°=∠ABF=∠BAF,推出AF=BF,设AF=BF=x,在Rt△AOF中,由∠AFO=90°,∠AOF=30°,推出OF=AF÷tan30°=$\sqrt{3}x$,可得方程2($\sqrt{3}$-1)+x=$\sqrt{3}$x,解得x=2,推出A(2$\sqrt{3}$,$\sqrt{3}$),再利用待定系数法即可解决问题.
(2)分两种情形求解①当∠BAE=∠AOE=30°,由∠AEB=∠AEO,推出△ABE∽△OAE,作EN⊥AB于N,设BE=x,则BN=NE=$\frac{\sqrt{2}}{2}$x,AN=$\sqrt{3}$NE=$\frac{\sqrt{6}}{2}$x,根据AB=$\sqrt{2}$AF=$\sqrt{6}$,可得$\frac{\sqrt{2}}{2}$x+$\frac{\sqrt{6}}{2}$x=$\sqrt{6}$,解方程即可.②当∠OAB=∠AE′B时,△ABE′∽△OBA,可以证明∠OAE′=∠AE′O=15°,推出OA=OE′=2AF=2$\sqrt{3}$,即可解决问题.
解答 解:(1)如图,作AF⊥OB于F.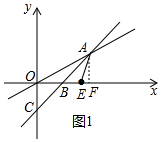
∵直线y=x-m与x轴交于点B,与y轴交于点C,
∴B(m,0),C(0,-m),
∴OC=OB,
∴∠OBC=∠OCB=45°=∠ABF=∠BAF,
∴AF=BF,设AF=BF=x,
在Rt△AOF中,∵∠AFO=90°,∠AOF=30°,
∴OF=AF÷tan30°=$\sqrt{3}x$,
∴2($\sqrt{3}$-1)+x=$\sqrt{3}$x,
∴x=2,
∴A(2$\sqrt{3}$,$\sqrt{3}$),
∵点A是直线y=x-m与直线y=kx的交点,
∴$\sqrt{3}$=2$\sqrt{3}$-m,
∴m=$\sqrt{3}$,
$\sqrt{3}$=2$\sqrt{3}$k,
∴k=$\frac{1}{2}$,
(2)如图2中,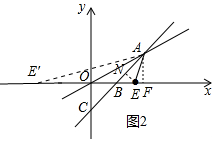
①当∠BAE=∠AOE=30°,∵∠AEB=∠AEO,
∴△ABE∽△OAE,作EN⊥AB于N,设BE=x,则BN=NE=$\frac{\sqrt{2}}{2}$x,AN=$\sqrt{3}$NE=$\frac{\sqrt{6}}{2}$x,
∵AB=$\sqrt{2}$AF=$\sqrt{6}$,
∴$\frac{\sqrt{2}}{2}$x+$\frac{\sqrt{6}}{2}$x=$\sqrt{6}$,
∴x=3-$\sqrt{3}$,
∴BE=3-$\sqrt{3}$,
∴OE=OB+BE=$\sqrt{3}$+3-$\sqrt{3}$=3,
∴E(3,0).
②当∠OAB=∠AE′B时,△ABE′∽△OBA,
∵∠ABF=∠AOB+∠OAB,∠ABF=45°,∠AOB=30°,
∴∠OAB=∠AE′O=15°,
∵∠AOB=∠AE′O+∠OAE′,
∴∠OAE′=∠AE′O=15°,
∴OA=OE′=2AF=2$\sqrt{3}$,
∴点E′的坐标为(-2$\sqrt{3}$,0),
综上所述,满足条件的点E的坐标为(3,0)或(-2$\sqrt{3}$,0).
点评 本题考查一次函数综合题、等腰直角三角形的性质、30度的直角三角形的性质、相似三角形的判定和性质等知识,解题的关键是熟练掌握待定系数法,学会用分类讨论的思想思考问题,属于中考压轴题.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 2009年我市荣获“国家卫生城市”称号,是全市人民共同努力的结果,可喜可贺!
2009年我市荣获“国家卫生城市”称号,是全市人民共同努力的结果,可喜可贺!查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a=5 | B. | a≥5 | C. | a=3 | D. | a≥3 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3cm,3cm,4cm | B. | 7cm,4cm,2cm | C. | 3cm,4cm,8cm | D. | 2cm,3cm,5cm |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com