
【题目】已知![]() 在平面直角坐标系中的位置如图所示,且三个顶点都在正方形网格的格点上.
在平面直角坐标系中的位置如图所示,且三个顶点都在正方形网格的格点上.
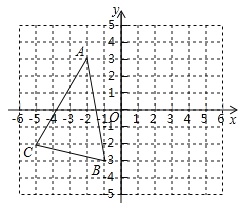
(1)把![]() 沿
沿![]() 轴翻折得到
轴翻折得到![]() ,画出
,画出![]() ,并写出点
,并写出点![]() 的坐标_____;
的坐标_____;
(2)若点![]() 在
在![]() 内部,当
内部,当![]() 沿
沿![]() 轴翻折后,点
轴翻折后,点![]() 对应点
对应点![]() 的坐标是_____;
的坐标是_____;
(3)求![]() 的面积.
的面积.
【答案】(1)如图见解析;![]() ;(2)
;(2)![]() ;(3)
;(3)![]() 的面积
的面积![]() .
.
【解析】
(1)根据网格特点得出A、B、C三点的对应点A′、B′、C′,顺次连接即可得△A′B′C′;根据关于y轴对称的点的坐标特征:纵坐标不变,横坐标互为相反数即可得A′坐标;
(2)根据关于y轴对称的点的坐标特征:纵坐标不变,横坐标互为相反数即可得答案;
(3)利用网格特点及勾股定理,用△ABC所在矩形的面积减去三个三角形的面积即可得答案.
(1)如图,△A′B′C′即为所求,
∵点A坐标为(-2,3),
∴点A关于y轴的对称点A′坐标为(2,3),

故答案为:(2,3)
(2)∵点P(m,n),
∴点![]() 关于y轴的对称点
关于y轴的对称点![]() 的坐标是(-m,n),
的坐标是(-m,n),
故答案为:(-m,n)
(3)∵A(-2,3),B(-1,-3),C(-5,-2),
∴△ABC的面积![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】小明从家出发沿一条笔直的公路骑自行车前往图书馆看书,他与图书馆之间的距离y(km)与出发时间t(h)之间的函数关系如图1中线段AB所示,在小明出发的同时,小明的妈妈从图书馆借书结束,沿同一条公路骑电动车匀速回家,两人之间的距离s(km)与出发时间t(h)之间的函数关系式如图2中折线段CD﹣DE﹣EF所示.
(1)小明骑自行车的速度为 km/h、妈妈骑电动车的速度为 km/h;
(2)解释图中点E的实际意义,并求出点E的坐标;
(3)求当t为多少时,两车之间的距离为18km.

查看答案和解析>>
科目:初中数学 来源: 题型:
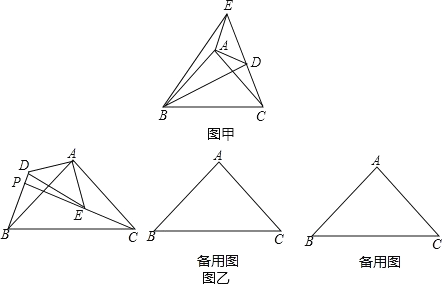
【题目】如图乙,△ABC 和△ADE 是有公共顶点的等腰直角三角形,∠BAC=∠DAE=90°,点P为射线 BD,CE的交点.
(1)如图甲,将△ADE 绕点A 旋转,当 C、D、E 在同一条直线上时,连接BD、BE,则下列给出的四个结论中,其中正确的是哪几个.(回答直接写序号)
①BD=CE;②BD⊥CE;③∠ACE+∠DBC=45°;④BE2=2(AD2+AB2)
(2)若 AB=4,AD=2,把△ADE 绕点 A 旋转,
①当∠CAE=90°时,求 PB 的长;
②直接写出旋转过程中线段 PB 长的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某市近郊有一块长为60米,宽为50米的矩形荒地,地方政府准备在此建一个综合性休闲广场,其中阴影部分为通道,通道的宽度均相等,中间的三个矩形(其中三个矩形的一边长均为a米)区域将铺设塑胶地面作为运动场地.设通道的宽度为x米.
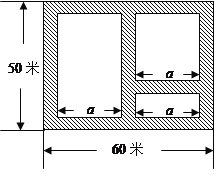
(1)a= (用含x的代数式表示);
(2)若塑胶运动场地总占地面积为 2430平方米,则通道的宽度为多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
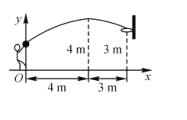
【题目】在一次篮球比赛中,如图队员甲正在投篮.已知球出手时离地面![]() m,与篮圈中心的水平距离为7 m,球出手后水平距离为4 m时达到最大高度4 m,设篮球运行轨迹为抛物线,篮圈距地面3 m.
m,与篮圈中心的水平距离为7 m,球出手后水平距离为4 m时达到最大高度4 m,设篮球运行轨迹为抛物线,篮圈距地面3 m.
(1)建立如图所示的平面直角坐标系,问此球能否准确投中?
(2)此时,对方队员乙在甲面前1 m处跳起盖帽拦截,已知乙的最大摸高为3.1 m,那么他能否获得成功?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】实验探究:
(1)如图1,对折矩形纸片ABCD,使AD与BC重合,得到折痕EF,把纸片展开;再一次折叠纸片,使点A落在EF上,并使折痕经过点B,得到折痕BM,同时得到线段BN,MN.请你观察图1,猜想∠MBN的度数是多少,并证明你的结论.
(2)将图1中的三角形纸片BMN剪下,如图2,折叠该纸片,探究MN与BM的数量关系,写出折叠方案,并结合方案证明你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:我们学过一次函数的图象的平移,如:将一次函数![]() 的图象沿
的图象沿![]() 轴向右平移
轴向右平移![]() 个单位长度可得到函数
个单位长度可得到函数![]() 的图象,再沿
的图象,再沿![]() 轴向上平移
轴向上平移![]() 个单位长度,得到函数
个单位长度,得到函数![]() 的图象;如果将一次函数
的图象;如果将一次函数![]() 的图象沿
的图象沿![]() 轴向左平移
轴向左平移![]() 个单位长度可得到函数
个单位长度可得到函数![]() 的图象,再沿
的图象,再沿![]() 轴向下平移
轴向下平移![]() 个单位长度,得到函数
个单位长度,得到函数![]() 的图象.类似地,形如
的图象.类似地,形如![]() 的函数图象的平移也满足此规律.
的函数图象的平移也满足此规律.
仿照上述平移的规律,解决下列问题:
(1)将一次函数![]() 的图象沿
的图象沿![]() 轴向右平移
轴向右平移![]() 个单位长度,再沿
个单位长度,再沿![]() 轴向上平移
轴向上平移![]() 个单位长度,得到函数________的图象(不用化简);
个单位长度,得到函数________的图象(不用化简);
(2)将![]() 的函数图象沿y轴向下平移
的函数图象沿y轴向下平移![]() 个单位长度,得到函数________________的图象,再沿
个单位长度,得到函数________________的图象,再沿![]() 轴向左平移
轴向左平移![]() 个单位长度,得到函数_________________的图象(不用化简);
个单位长度,得到函数_________________的图象(不用化简);
(3)函数![]() 的图象可看作由
的图象可看作由![]() 的图象经过怎样的平移变换得到?
的图象经过怎样的平移变换得到?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一家用电器开发公司研制出一种新型电子产品,每件的生产成本为18元,按定价40元出售,每月可销售20万件![]() 为了增加销量,公司决定采取降价的办法,经市场调研,每降价1元,月销售量可增加2万件.
为了增加销量,公司决定采取降价的办法,经市场调研,每降价1元,月销售量可增加2万件.
![]() 求出月销售量
求出月销售量![]() 万件
万件![]() 与销售单价
与销售单价![]() 元
元![]() 之间的函数关系式;
之间的函数关系式;
![]() 求出月销售利润
求出月销售利润![]() 万元
万元![]() 与销售单价
与销售单价![]() 元
元![]() 之间的函数关系式;
之间的函数关系式;
![]() 若该月销售利润为480万元,求此时的月销售量和销售单价各是多少元?
若该月销售利润为480万元,求此时的月销售量和销售单价各是多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com