
【题目】如图,在平面直角坐标系中,点A坐标为(0,3),点B在x轴上
(1)在坐标系中求作一点M,使得点M到点A,点B和原点O这三点的距离相等,在图中保留作图痕迹,不写作法;
(2)若sin∠OAB=![]() ,求点M的坐标;
,求点M的坐标;
(3)在(2)的条件下,直接写出以点O、M、B为其中三个顶点的平行四边形的第四个顶点P的坐标

【答案】(1)详见解析;(2)(2,![]() );(3)P(6,1.5)或P(﹣2,1.5)或P(2,﹣1.5)
);(3)P(6,1.5)或P(﹣2,1.5)或P(2,﹣1.5)
【解析】
(1)直接利用线段垂直平分线的作法结合直角三角形的性质得出答案;
(2)利用勾股定理得出OB的长,再利用M点为AB的中点即可得出其坐标.
(3)根据平行四边形的性质直接得出P的坐标即可.
(1)如图所示:点M,即为所求;
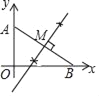
(2)∵sin∠OAB=![]() ,
,
∴设OB=4x,AB=5x,
由勾股定理可得:32+(4x)2=(5x)2,
解得:x=1,
由作图可得:M为AB的中点,则M的坐标为:(2,![]() ).
).
(3)∵B(4,0),M(2,![]() ),OMBP是平行四边形,
),OMBP是平行四边形,
∴MP∥x轴,
∴P的纵坐标为1.5,MP=4,
可得:P(6,1.5)或P(﹣2,1.5),
∵当OP∥MB时,
∴P(2,﹣1.5),
综上所述:P(6,1.5)或P(﹣2,1.5)或P(2,﹣1.5),


 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,D为AB中点,AE∥CD,CE∥AB.
(1)试判断四边形ADCE的形状,并证明你的结论.
(2)连接BE,若∠BAC=30°,CE=1,求BE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某文具店准备购进A、B两种品牌的文具袋进行销售,若购进A品牌文具袋和B品牌文具袋各5个共花费120元,购进A品牌文具袋3个和B品牌文具袋4个共花费88元.
(1)求购进A品牌文具袋和B品牌文具袋的单价;
(2)若该文具店购进了A,B两种品牌的文具袋共100个,其中A品牌文具袋售价为12元,B品牌文具袋售价为23元,设购进A品牌文具袋x个,获得总利润为w元.
①求w关于x的函数关系式;
②要使销售文具袋的利润最大,且所获利润不低于进货价格的45%,请你帮该文具店设计一个进货方案,并求出其所获利润的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
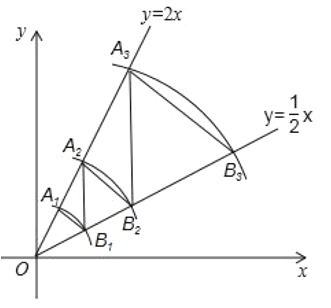
【题目】如图,在平面直角坐标系中,点A1的坐标为(1,2),以点O为圆心,以OA1长为半径画弧,交直线![]() 于点B1.过B1点作B1A2∥y轴,交直线y=2x于点A2,以O为圆心,以OA2长为半径画弧,交直线
于点B1.过B1点作B1A2∥y轴,交直线y=2x于点A2,以O为圆心,以OA2长为半径画弧,交直线![]() 于点B2;过点B2作B2A3∥y轴,交直线y=2x于点A3,以点O为圆心,以OA3长为半径画弧,交直线
于点B2;过点B2作B2A3∥y轴,交直线y=2x于点A3,以点O为圆心,以OA3长为半径画弧,交直线![]() 于点B3;过B3点作B3A4∥y轴,交直线y=2x于点A4,以点O为圆心,以OA4长为半径画弧,交直线
于点B3;过B3点作B3A4∥y轴,交直线y=2x于点A4,以点O为圆心,以OA4长为半径画弧,交直线![]() 于点B4,…按照如此规律进行下去,点B2020的坐标为__________.
于点B4,…按照如此规律进行下去,点B2020的坐标为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
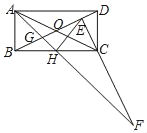
【题目】如图,矩形ABCD中,BC=2AB,对角线相交与O点,过C点作CE⊥BD交BD于E点,H为BC中点,连接AH交BD于G点,交EC的延长线于F点,下列4个结论:①EH=AB;②∠ABG=∠HEC;③△ABG≌△HEC;④CF=BD.正确的结论是( )
A.①②④B.①④C.③④D.①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知抛物线y=﹣x2+2x+3与x轴交于A、B两点,与y轴交于点C,顶点为D,连接BC
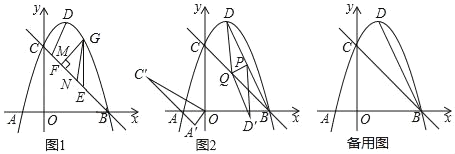
(1)点G是直线BC上方抛物线上一动点(不与B、C重合),过点G作y轴的平行线交直线BC于点E,作GF⊥BC于点F,点M、N是线段BC上两个动点,且MN=EF,连接DM、GN.当△GEF的周长最大时,求DM+MN+NG的最小值;
(2)如图2,连接BD,点P是线段BD的中点,点Q是线段BC上一动点,连接DQ,将△DPQ沿PQ翻折,且线段D′P的中点恰好落在线段BQ上,将△AOC绕点O逆时针旋转60°得到△A′OC′,点T为坐标平面内一点,当以点Q、A′、C′、T为顶点的四边形是平行四边形时,求点T的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解学生的安全意识情况,在全校范围内随机抽取部分学生进行问卷调查,根据调查结果,把学生的安全意识分成“淡薄”“一般”“较强”“很强”四个层次,并绘制成如下两幅尚不完整的统计图
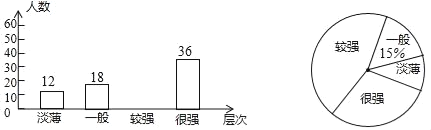
根据以上信息,解答下列问题:
(1)该校有1200名学生,现要对安全意识为“淡薄”、“一般”的学生强化安全教育,根据调查结果,估计全校需要强化安全教育的学生约有多少名?
(2)请直接将条形统计图补充完整.
查看答案和解析>>
科目:初中数学 来源: 题型:
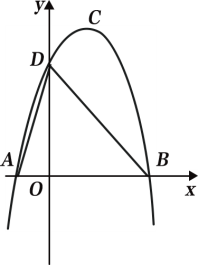
【题目】如图1,抛物线![]() 的顶点为C(1,4),交x轴于A、B两点,交y轴于点D,其中点B的坐标为(3,0).
的顶点为C(1,4),交x轴于A、B两点,交y轴于点D,其中点B的坐标为(3,0).
(1)求抛物线的解析式;
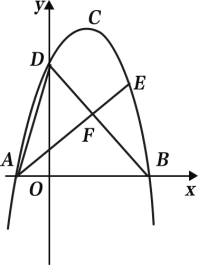
(2)如图2,点E是BD上方抛物线上的一点,连接AE交DB于点F,若AF=2EF,求出点E的坐标.
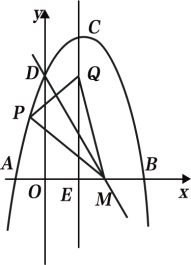
(3)如图3,点M的坐标为(![]() ,0),点P是对称轴左侧抛物线上的一点,连接MP,将MP沿MD折叠,若点P恰好落在抛物线的对称轴CE上,请求出点P的横坐标.
,0),点P是对称轴左侧抛物线上的一点,连接MP,将MP沿MD折叠,若点P恰好落在抛物线的对称轴CE上,请求出点P的横坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com