
| 1 |
| 2 |

| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
|
|
|
| 9 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
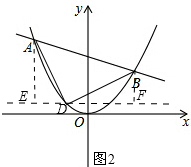
| AE |
| DF |
| ED |
| FB |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| AE |
| DF |
| ED |
| FB |
| ||||
| n-t |
| t-m | ||||
|
| (m+t)(m-t) |
| 2(n-t) |
| 2(t-m) |
| (n+t)(n-t) |
| m+t |
| 2 |
| -2 |
| n+t |
| 1 |
| 2 |
| 1 |
| 2 |

| GC2+DG2 |
| 22+42 |
| 20 |
| 5 |
| 5 |
| 5 |
| 5 |


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
| OD |
| AD |
| OE |
| CE |
| OF |
| BF |
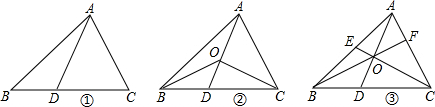
查看答案和解析>>
科目:初中数学 来源: 题型:
| 3 |
| 2 |
| ||
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
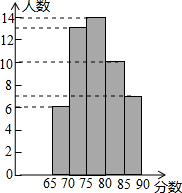 某公司招聘人才,对应聘者分别进行阅读能力、思维能力和表达能力三项测试,其中甲、乙两人的成绩如下表(单位:分):
某公司招聘人才,对应聘者分别进行阅读能力、思维能力和表达能力三项测试,其中甲、乙两人的成绩如下表(单位:分):| 项目 人员 | 阅读 | 思维 | 表达 |
| 甲 | 93 | 86 | 73 |
| 乙 | 95 | 81 | 79 |
查看答案和解析>>
科目:初中数学 来源: 题型:
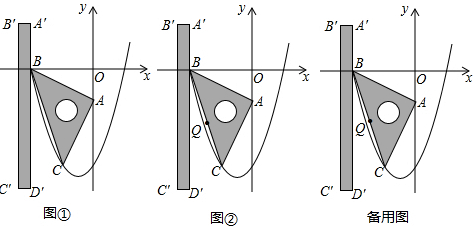
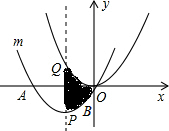 如图,把抛物线y=
如图,把抛物线y=| 1 |
| 2 |
| 1 |
| 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com