
【题目】(本小题满分14分)
如图,直线y=kx+b(k、b为常数)分别与x轴、y轴交于点A(-4,0)、B(0,3),抛物线y=-x2+2x+1与y轴交于点C.
(1)求直线y=kx+b的解析式;
(2)若点P(x,y)是抛物线y=-x2+2x+1上的任意一点,设点P到直线AB的距离为d,求d关于x的函数解析式,并求d取最小值时点P的坐标;
(3)若点E在抛物线y=-x2+2x+1的对称轴上移动,点F在直线AB上移动,求CE+EF的最小值. 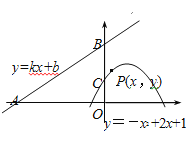
【答案】(1) y=![]() x+3;(2)P(
x+3;(2)P(![]() ,
,![]() );(3)
);(3)![]() .
.
【解析】
试题分析:(1)将A、B两点坐标代入y=kx+b中,求出k、b的值;(2)作出点P到直线AB的距离后,由于∠AHC=90°,考虑构造“K形”相似,得到△MAH、△OBA、△NHP三个三角形两两相似,三边之比都是3∶4∶5.由“![]() ”可得
”可得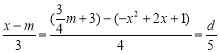 ,整理可得d关于x的二次函数,配方可求出d的最小值;(3)如果点C关于直线x=1的对称点C′,根据对称性可知,CE=C′E.当C′F⊥AB时,CE+EF最小.
,整理可得d关于x的二次函数,配方可求出d的最小值;(3)如果点C关于直线x=1的对称点C′,根据对称性可知,CE=C′E.当C′F⊥AB时,CE+EF最小.
试题解析:
解:(1)∵y=kx+b经过A(-4,0)、B(0,3),
∴![]() ,解得k=
,解得k=![]() ,b=3.
,b=3.
∴y=![]() x+3.
x+3.
(2)过点P作PH⊥AB于点H,过点H作x轴的平行线MN,分别过点A、P作MN的垂线段,垂足分别为M、N.
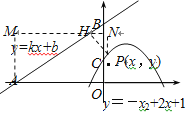
设H(m,![]() m+3),则M(-4,
m+3),则M(-4,![]() m+3),N(x,
m+3),N(x,![]() m+3),P(x,-x2+2x+1).
m+3),P(x,-x2+2x+1).
∵PH⊥AB,∴∠CHN+∠AHM=90°,∵AM⊥MN,∴∠MAH+∠AHM=90°.
∴∠MAH=∠CHN,∵∠AMH=∠CNH=90°,∴△AMH∽△HNP.
∵MA∥y轴,∴△MAH∽△OBA.∴△OBA∽△NHP.
∴![]() .
.
∴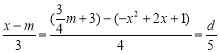 .
.
整理得:![]() ,所以当x=
,所以当x=![]() ,即P(
,即P(![]() ,
,![]() ).
).
(3)作点C关于直线x=1的对称点C′,过点C′作C′F⊥AB于F.过点F作JK∥x轴,,分别过点A、C′作J⊥JK于点J,C′K⊥JK于点K.则C′(2,1)
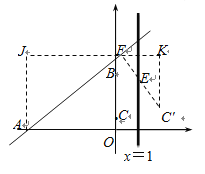
设F(m,![]() m+3)
m+3)
∵C′F⊥AB,∠AFJ+∠C′FK=90°,∵CK⊥JK,∴∠C′+∠C′FK=90°.
∴∠C′=∠AFJ,∵∠J=∠K=90°,∴△AFJ∽△FC′K.
∴![]() ,∴
,∴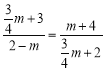 ,解得m=
,解得m=![]() 或-4(不符合题意).
或-4(不符合题意).
∴F(![]() ,
,![]() ),∵C′(2,1),∴FC′=
),∵C′(2,1),∴FC′=![]() .
.
∴CE+EF的最小值=C′E=![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】已知一次函数y=kx+b的图象经过点A(﹣3,0),B(2,5)两点.正比例函数y=kx的图象经过点B(2,3).
(1)求这两个函数的表达式.
(2)在直角坐标系中,画出这个函数的图象.
(3)求三角形AOB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
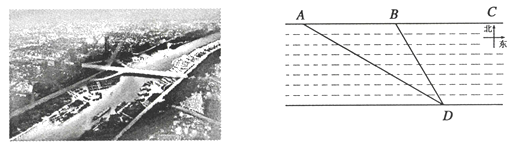
【题目】如图,建设“幸福西宁”,打造“绿色发展样板城市”.美丽的湟水河宛如一条玉带穿城而过,已形成“水清、流畅、岸绿、景美”的生态环境新格局.在数学课外实践活动中,小亮在海湖新区自行车绿道北段![]() 上的
上的![]() 两点分别对南岸的体育中心
两点分别对南岸的体育中心![]() 进行测量,分别没得
进行测量,分别没得![]() 米,求体育中心
米,求体育中心![]() 到湟水河北岸
到湟水河北岸![]() 的距离约为多少米(精确到1米,
的距离约为多少米(精确到1米,![]() )?
)?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了从甲、乙两名选手中选拔一个参加射击比赛,现对他们进行一次测验,两个人在相同条件下各射靶10次,为了比较两人的成绩,制作了如下统计图:
甲、乙射击成绩统计表
平均数 | 中位数 | 方差 | 命中10环的次数 | |
甲 | 7 | 4 | 0 | |
乙 | 5.4 | 1 |
甲、乙射击成绩折线图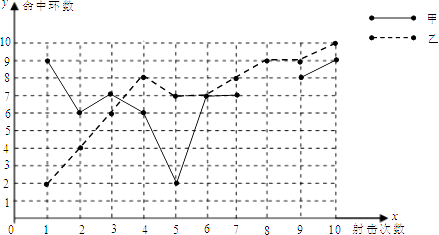
(1)请计算出甲选手第8次命中的环数;
(2)补全上述图表(请直接在表中填空和补全折线图);
(3)你会选择哪位选手参加比赛?说说你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将△ABC沿直线AB翻折后得到△ABC1 , 再将△ABC绕点A旋转后得到△AB2C2 , 对于下列两个结论: 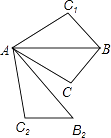
①“△ABC1能绕一点旋转后与△AB2C2重合”;
②“△ABC1能沿一直线翻折后与△AB2C2重合”的正确性是( )
A.结论①、②都正确
B.结论①、②都错误
C.结论①正确、②错误
D.结论①错误、②正确
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着新农村的建设和旧城的改造,我们的家园越来越美丽,小明家附近广场中央新修了一个圆形喷水池,在水池中心竖直安装了一根高![]() 米的喷水管,它喷出的抛物线形水柱在与池中心的水平距离为米处达到最高,水柱落地处离池中心
米的喷水管,它喷出的抛物线形水柱在与池中心的水平距离为米处达到最高,水柱落地处离池中心![]() 米.
米.

(1)请你建立适当的直角坐标系,并求出水柱抛物线的函数解析式;
(2)求出水柱的最大高度是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店经销一种双肩包,已知这种双肩包的成本价为每个30元.市场调查发现,这种双肩包每天的销售量y(单位:个)与销售单价x(单位:元)有如下关系:y=-x+60(30≤x≤60).
设这种双肩包每天的销售利润为w元.
(1)求w与x之间的函数解析式;
(2)这种双肩包销售单价定为多少元时,每天的销售利润最大?最大利润是多少元?
(3)如果物价部门规定这种双肩包的销售单价不高于48元,该商店销售这种双肩包每天要获得200元的销售利润,销售单价应定为多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com