
 长为
长为 .
.
 的中点M.求证:AF=AB;
的中点M.求证:AF=AB;
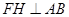 于H,由AB为直径可得∠ACB=90°,即可求得∠A的度数,再根据含30°角的直角三角形的可得到
于H,由AB为直径可得∠ACB=90°,即可求得∠A的度数,再根据含30°角的直角三角形的可得到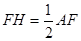 ,由点M为
,由点M为 的中点可得OM⊥AB且OM =
的中点可得OM⊥AB且OM =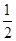 AB,再根据△ABC与△FED全等可得∠A=∠EFD=30°,即可证得结论;(3)
AB,再根据△ABC与△FED全等可得∠A=∠EFD=30°,即可证得结论;(3)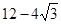
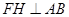 于H,由AB为直径可得∠ACB=90°,即可求得∠A的度数,再根据含30°角的直角三角形的性质可得到
于H,由AB为直径可得∠ACB=90°,即可求得∠A的度数,再根据含30°角的直角三角形的性质可得到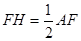 ,由点M为
,由点M为 的中点可得OM⊥AB且OM =
的中点可得OM⊥AB且OM =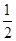 AB,再根据△ABC与△FED全等可得∠A=∠EFD=30°,即可证得结论;
AB,再根据△ABC与△FED全等可得∠A=∠EFD=30°,即可证得结论;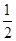
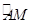 =45°可得MN=NC=x,在Rt△AMN中,根据勾股定理即可列方程求得x的值,最后根据三角形的面积公式求解即可.
=45°可得MN=NC=x,在Rt△AMN中,根据勾股定理即可列方程求得x的值,最后根据三角形的面积公式求解即可. 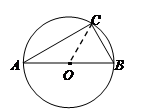
 长为
长为 ,⊙O的半径为4cm
,⊙O的半径为4cm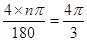 ,解得n=60,即∠BOC="60"
,解得n=60,即∠BOC="60" 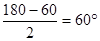 ;
;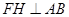 于H
于H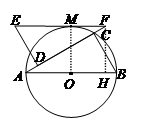
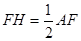
 的中点
的中点 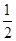 AB
AB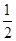 AB
AB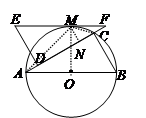
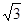
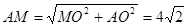
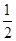
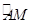 =45°
=45° 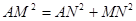
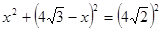
 ,
,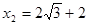 (舍去)
(舍去)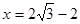
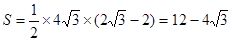 .
.

科目:初中数学 来源:不详 题型:解答题

 ,求AD的长.
,求AD的长.查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题

查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
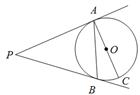
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
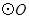 是Rt
是Rt ABC的外接圆,
ABC的外接圆,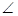 ABC=90
ABC=90 ,点P是
,点P是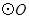 外一点,PA切
外一点,PA切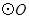 于点A,且PA=PB.
于点A,且PA=PB.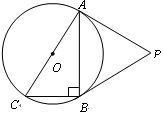
 的切线;
的切线;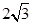 ,BC=2,求
,BC=2,求 的半径.
的半径.查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 中,半径长
中,半径长 ,
, ;以
;以 为直径作半圆
为直径作半圆 ,点
,点 是弧
是弧 上的一个动点,
上的一个动点, 与半圆
与半圆 交于点
交于点 ,
, ⊥
⊥ 于点
于点 ,
, 与
与 交于点
交于点 ,连结
,连结 .
.
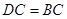 ;
; ,
,  ,试求
,试求 关于
关于 的函数关系式,并写出
的函数关系式,并写出 的取值范围;
的取值范围; 落在线段
落在线段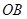 上,当
上,当 ∽
∽ 时,求线段
时,求线段 的长度.
的长度. 查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com