
分析 (1)根据:年利润=(售价-进价)×年销售量-每年的广告费,可列函数解析式;
(2)将(1)中函数解析式配方成顶点式,根据二次函数的性质即可得答案;
(3)由(2)中顶点式即可得最值情况.
解答 解:(1)S=(3-2)×10y-x
=-10x2+10x+10-x
=-10x2+9x+10;
(2)∵S=-10x2+9x+10=-10(x-$\frac{9}{20}$)2+$\frac{481}{40}$,
∴当0<x<$\frac{9}{20}$时,S随x的增大而增大,
答:广告费在0~$\frac{9}{20}$范围内,公司获得的年利润随广告费的增大而增大;
(3)由(2)知,当x=$\frac{9}{20}$时,S取得最大值,为$\frac{481}{40}$万元,
答:投入的广告费为$\frac{9}{20}$万元时,公司获得的年利润最大,是$\frac{481}{40}$万元.
点评 本题主要考查二次函数的应用,根据题意找到题目蕴含的相等关系列出函数解析式,并熟练掌握二次函数的性质是解题的关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
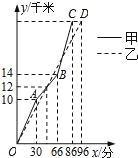 在一次自行车越野赛中,甲乙两名选手行驶的路程y(千米)随时间x(分)变化的图象(全程)如图,根据图象判定下列结论不正确的是( )
在一次自行车越野赛中,甲乙两名选手行驶的路程y(千米)随时间x(分)变化的图象(全程)如图,根据图象判定下列结论不正确的是( )| A. | 前30分钟,甲在乙的前面 | B. | 这次比赛的全程是28千米 | ||
| C. | 第48分钟时,两人第一次相遇 | D. | 甲先到达终点 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (1,3) | B. | (-1,-3) | C. | (-1,3) | D. | (3,1) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
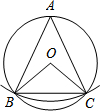 如图,AB是⊙O的弦(AB不是直径),以点A为圆心,以AB长为半径画弧交⊙O于点C,连结AC、BC、OB、OC.若∠ABC=65°,则∠BOC的度数是( )
如图,AB是⊙O的弦(AB不是直径),以点A为圆心,以AB长为半径画弧交⊙O于点C,连结AC、BC、OB、OC.若∠ABC=65°,则∠BOC的度数是( )| A. | 50° | B. | 65° | C. | 100° | D. | 130° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
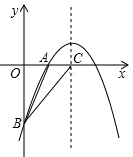 如图,已知二次函数y=-$\frac{1}{2}$x2+bx-6的图象与x轴交于一点A(2,0),与y轴交于点B,对称轴与x轴交于点C,连接BA、BC,求△ABC的面积.
如图,已知二次函数y=-$\frac{1}{2}$x2+bx-6的图象与x轴交于一点A(2,0),与y轴交于点B,对称轴与x轴交于点C,连接BA、BC,求△ABC的面积.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com