
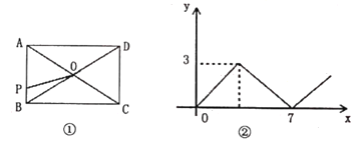
【题目】如图①,在矩形ABCD中,AB<AD,对角线AC,BD相交于点O,动点P由点A出发,沿AB-BC→CD向点D运动设点P的运动路程为x,△AOP的面积为y,y与x的函数关系图象如图②所小示,则AD的长为________.
【答案】4
【解析】
当P点在AB上运动时,△AOP面积逐渐增大,当P点到达B点时,结合图象可得△AOP面积最大为3,得到AB与BC的积为12;当P点在BC上运动时,△AOP面积逐渐减小,当P点到达C点时,△AOP面积为0,此时结合图象可知P点运动路径长为7,得到AB与BC的和为7,构造关于AB的一元二方程可求解.
①当点P在AB上运动时,y=![]() AP·×
AP·×![]() AD
AD
由图象可知:△AOP面积逐渐增大,当P点到达B点时,△AOP面积最大为3,此时 y=![]() AB×
AB×![]() BC=
BC=![]() AB·BC=3,即AB·BC=12;
AB·BC=3,即AB·BC=12;
②当P点在BC上运动时,△AOP面积逐渐减小,当P点到达C点时,由图象可知,此时△AOP面积的为0,P点运动路径长为7,即AB+BC=7
∴BC=7-AB,代入ABBC=12,得:
AB(7-AB)=12,解得AB=4或3
又∵AB<AD,即AB<BC
∴AB=3,BC=4.
∴AD=4
故答案为:4


 巧学巧练系列答案
巧学巧练系列答案科目:初中数学 来源: 题型:
【题目】心理学家发现:课堂上,学生对概念的接受能力s与提出概念的时间t(单位:min)之间近似满足函数关系s=at2+bt+c(a≠0),s值越大,表示接受能力越强.如图记录了学生学习某概念时t与s的三组数据,根据上述函数模型和数据,可推断出当学生接受能力最强时,提出概念的时间为( )
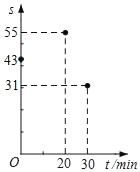
A. 8min B. 13min C. 20min D. 25min
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:
在数学课上,老师提出如下问题:
尺规作图:作Rt△ABC,使其斜边AB=c,一条直角边BC=a.
已知线段a,c如图.

小芸的作法如下:
① 取AB=c,作AB的垂直平分线交AB于点O; ② 以点O为圆心,OB长为半径画圆;
③ 以点B为圆心,a长为半径画弧,与⊙O交于点C;④ 连接BC,AC.
则Rt△ABC即为所求.老师说:“小芸的作法正确.”
请回答:小芸的作法中判断∠ACB是直角的依据是________________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)计算:(3﹣π)0﹣![]() +|3﹣
+|3﹣![]() |+(tan30°)﹣1
|+(tan30°)﹣1
(2)定义新运算:对于任意实数a,b,都有a⊕b=a(a﹣b)+1,等式右边是通常的加法、减法及乘法运算.比如:2⊕5=2×(2﹣5)+1
=2×(﹣3)+1
=﹣6+1
=﹣5
若3⊕x的值小于13,求x的取值范围,并在如图所示的数轴上表示出来.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=12,点D在边BC上,点E在线段AD上,EF⊥AC于点F,EG⊥EF交AB于点G,若EF=EG,则CD的长为( )
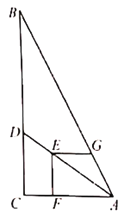
A.3.6B.4C.4.8D.5
查看答案和解析>>
科目:初中数学 来源: 题型:
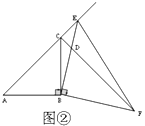
【题目】如图,已知![]() ,点
,点![]() 为直线
为直线![]() 上一点,以
上一点,以![]() 为边,点
为边,点![]() 为直角顶点作等腰直角三角形
为直角顶点作等腰直角三角形![]() .
.
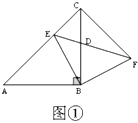
(1)如图①,当点![]() 在线段
在线段![]() 上时,
上时,![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ;
;
①找出一对全等三角形为_____________;
②若四边形![]() 的面积为7,则
的面积为7,则![]() 的长是_______.
的长是_______.
(2)如图②,当点![]() 在
在![]() 的延长线上时,
的延长线上时,![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() .
.
①![]() 的面积记为
的面积记为![]() ,
,![]() 的面积记为
的面积记为![]() ,探究
,探究![]() 、
、![]() 之间的数量关系并说明理由;
之间的数量关系并说明理由;
②当![]() 的面积为1时,求
的面积为1时,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点E是正方形ABCD的边BC延长线上一点,连接DE,过顶点B作BF⊥DE,垂足为F,BF交边DC于点G.
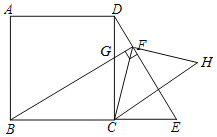
(1)求证:DGBC=DFBG;
(2)连接CF,求∠CFB的大小;
(3)作点C关于直线DE的对称点H,连接CH,FH.猜想线段DF,BF,CH之间的数量关系并加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
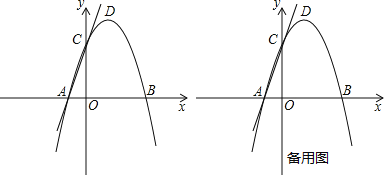
【题目】如图,在平面直角坐标系中,抛物线y=ax2+2x+c与x轴交于A(﹣1,0)B(3,0)两点,与y轴交于点C,点D是该抛物线的顶点.
(1)求抛物线的解析式和直线AC的解析式;
(2)请在y轴上找一点M,使△BDM的周长最小,求出点M的坐标;
(3)试探究:在拋物线上是否存在点P,使以点A,P,C为顶点,AC为直角边的三角形是直角三角形?若存在,请求出符合条件的点P的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com