
【题目】二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论正确的是( ) 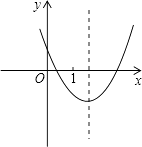
A.ac<0
B.当x=1时,y>0
C.方程ax2+bx+c=0(a≠0)有两个大于1的实数根
D.存在一个大于1的实数x0 , 使得当x<x0时,y随x的增大而减小;当x>x0时,y随x的增大而增大
【答案】D
【解析】解:A、抛物线开口向上,a>0,抛物线与y轴交于正半轴,c>0,所以ac>0,错误;
B、由图象可知,当x=1时,y<0,错误;
C、方程ax2+bx+c=0(a≠0)有一个根小于1,一个根大于1,错误;
D、由于函数图象的对称轴在x=1的右侧,所以存在一个大于1的实数x0 , 使得当x<x0时,y随x的增大而减小;当x>x0时,y随x的增大而增大,正确.
故选D.
【考点精析】解答此题的关键在于理解二次函数的性质的相关知识,掌握增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小.


科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c的图象交x轴于A、B两点,交y轴于点C,且B(1,0),C(0,3),将△BOC绕点O按逆时针方向旋转90°,C点恰好与A重合.
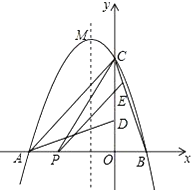
(1)求该二次函数的解析式;
(2)若点P为线段AB上的任一动点,过点P作PE∥AC,交BC于点E,连结CP,求△PCE面积S的最大值;
(3)设抛物线的顶点为M,Q为它的图象上的任一动点,若△OMQ为以OM为底的等腰三角形,求Q点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示是二次函数y=﹣ ![]() x2+2的图象在x轴上方的一部分,对于这段图象与x轴所围成的阴影部分的面积,你认为与其最接近的值是( )
x2+2的图象在x轴上方的一部分,对于这段图象与x轴所围成的阴影部分的面积,你认为与其最接近的值是( ) 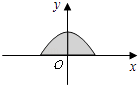
A.4
B.![]()
C.2π
D.8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若(3x﹣1)5=a0+a1x+a2x2+…+a5x5 , 则a1+2a2x+3a3x+4a4+5a5=( )
A.80
B.120
C.180
D.240
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年“五一”节,小明外出爬山,他从山脚爬到山顶的过程中,中途休息了一段时间.设他从山脚出发后所用的时间为t(分钟),所走的路程为s(米),s与t之间的函数关系如图所示,下列说法错误的是( )

A.小明中途休息用了20分钟
B.小明休息前爬山的平均速度为每分钟70米
C.小明在上述过程中所走的路程为6600米
D.小明休息前爬山的平均速度大于休息后爬山的平均速度
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了估计水塘中的鱼数,养鱼者先从鱼塘中捕获30条鱼,在每一条鱼身上做好标记后把这些鱼放归鱼塘,再从鱼塘中打捞鱼。通过多次实验后发现捕捞的鱼中有作记号的频率稳定在2.5%左右,则鱼塘中鱼的条数估计为( )
A.600条B.1200条C.2200条D.3000条
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC在平面直角坐标系中的位置如图1所示,A点坐标为(![]() ,0),B点坐标为(6,0),点D为AC的中点,点E是抛物线在第二象限图像上一动点,经过点A、B、C三点的抛物线的解析式为
,0),B点坐标为(6,0),点D为AC的中点,点E是抛物线在第二象限图像上一动点,经过点A、B、C三点的抛物线的解析式为![]() .
.
(1)求抛物线的解析式;
(2)如图1,连接DE,把点A沿直线DE翻折,点A的对称点为点G,当点G恰好落在抛物线的对称轴上时,求G点的坐标;
(3)图2中,点E运动时,当点G恰好落在BC上时,求E点的坐标.


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com